• Optimizer 와 Loss의 관계
  • 1. Momentum (1980s–1990s 전통 최적화에서 도입)
  • 2. Nesterov Accelerated Gradient (NAG, 2000s)
  • 3. AdaGrad (2011)
  • 4. RMSProp (2012, Hinton) 힌튼햄 입갤ㄷㄷ;
  • 5. Adam (2015)
  • 6. AdamW (2017)
• 최신 기법 (AdamW8bit, Adafactor, Lion, Prodigy)
  • AdamW8bit
  • Adafactor (T5 학습에 채택됨)
    • 2차 모멘텀을 “행/열 factorization”으로 저장
    • 1차 모멘텀($m_t$) 자체를 없앰
    • Learning rate도 파라미터 크기에 따라 자동 조절
    • 종합 장/단점.
  • Lion Optimizer
  • Prodigy Optimizer
    • My 실험 내용 해석

아래의 그래프들은 LoRA 학습할 때 내가 겪은 다양한 Prodigy Optimizer의 lr 스케줄링 변화 그래프다.

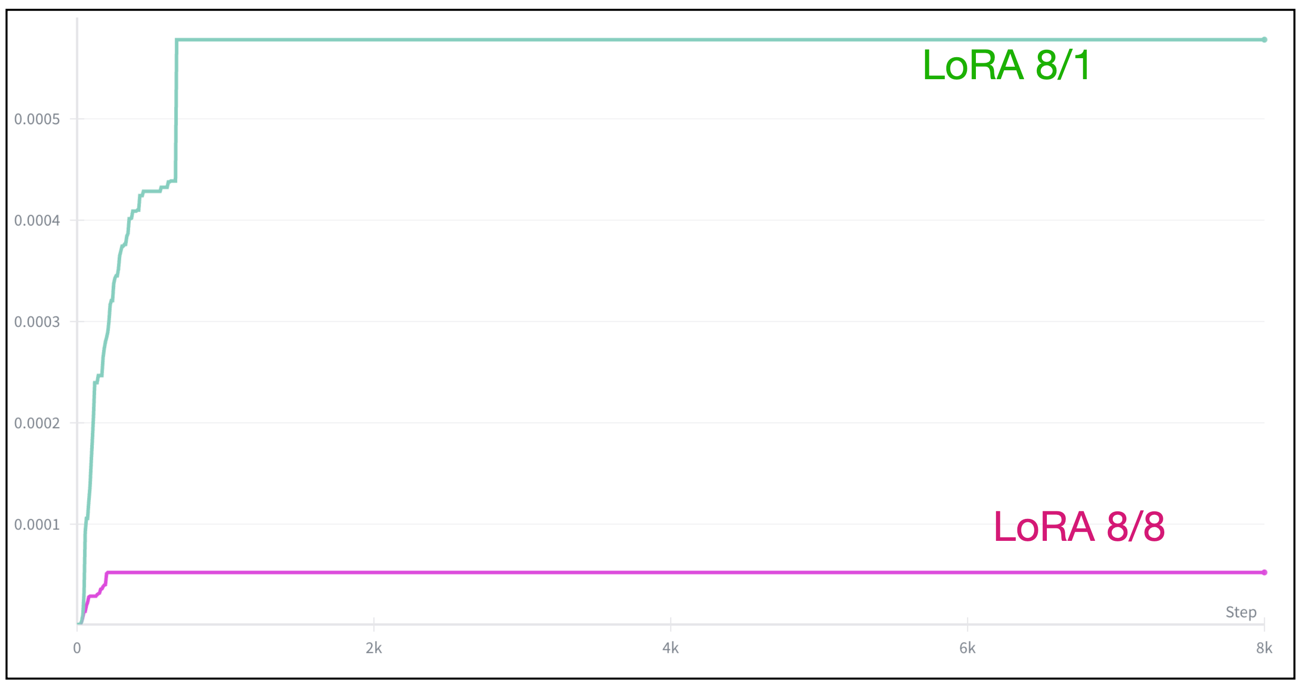
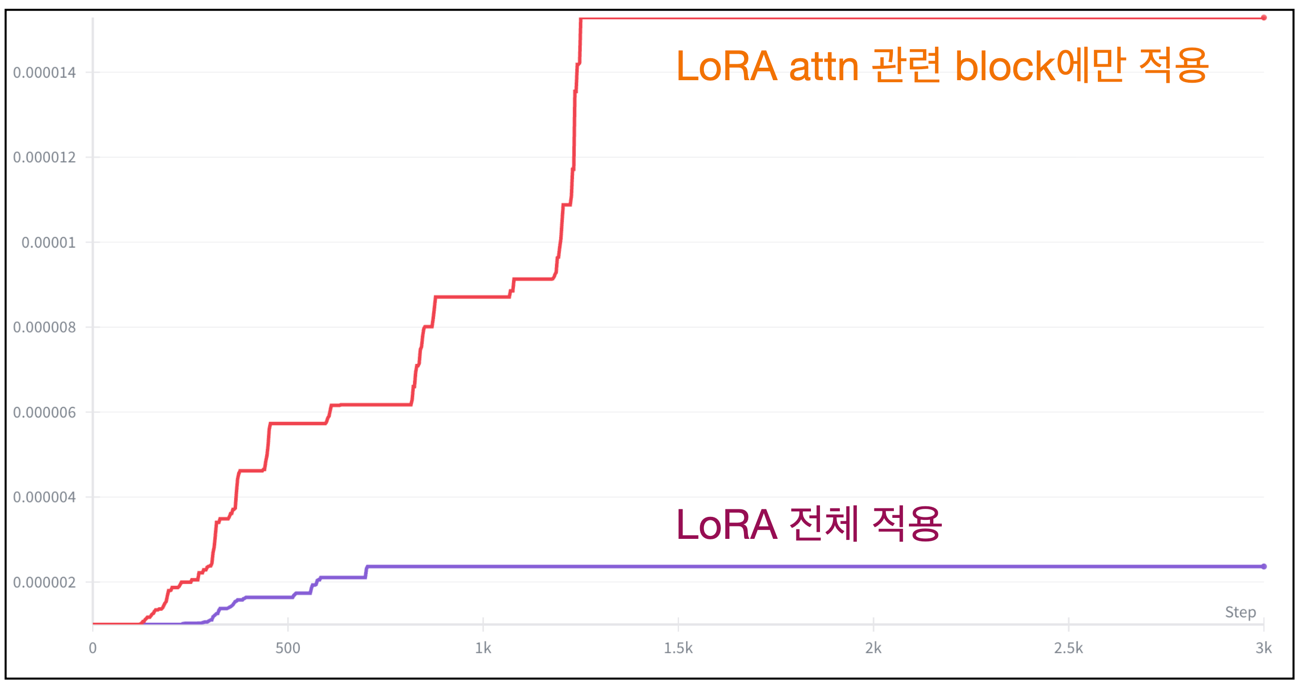
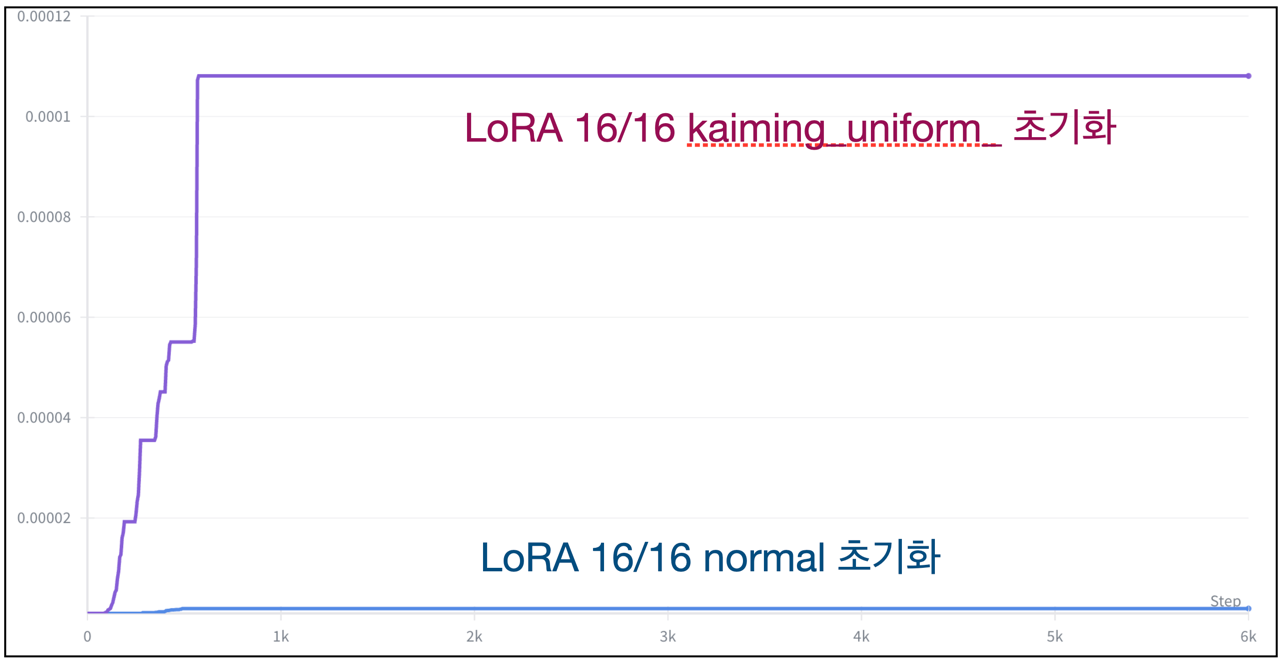
Omini-control 만지며 처음알게 된 optimizer로 LR 스케줄링을 지가 알아서 해준다 (삼성과 메타 직원이 저자임 ㄷㄷ;). 나의 스승 kohya는 Diffusion 학습할 때 adafactor, adamw8bit 을 애용하는듯 하지만, prodigy를 써본 후 lr을 수동으로 조절해줘야하는 저 optimizer들은 사용하기 겁난다.
그러나 뭔가 저 lr 이 올라가는 기준을 모르니 왠지모르게 답답하고, 완벽하게 이용하지 못하고 있는듯하다. 그래서 ChatGPT한테 알려달라했었는데 optimizer 기본 개념이 너무 부족하다보니 하나도 이해를 못했다 (논문 수식도 상당히 빡새보여서 보려면 1달정도 잡아야함).
따라서 학부 때 대충 파악하고 (사실 거의 모멘텀 적용 optimizer부터 이해못함) 넘어갔던 optimizer 개념을 좀 잡은 후 prodigy, adamW, adafactor, adamW8bit 등 Diffusion 학습에 자주 보이는 optimizer를 파보려고한다.

Optimizer 와 Loss의 관계

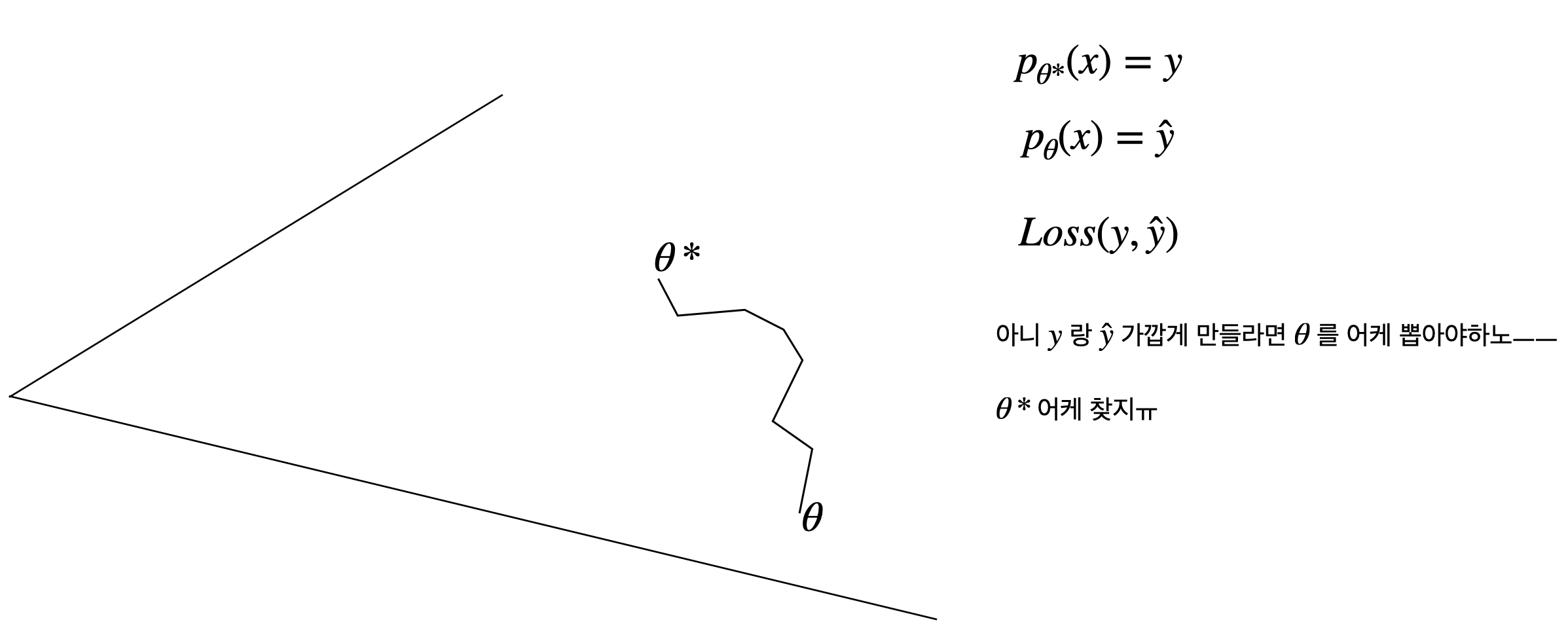우선 현재 내 머리속에 들어있는 Loss와 optimizer의 관계다. likelihood 기반 loss 기준으로 $\theta$를 어떻게 만져나가야 loss를 줄일 수 있을지, $\theta$의 변화 방향을 제시하는 세르파가 optimizer다.

• 근데 좀 의문인점이 보통 이 $\theta$ surface를 convex로 잡고 가던데, $\theta$가 최적점에 가까워질 때 loss가 작아져야만 그게 성립할텐데 무조건 성립하는가?
• \(d(\theta^*, \theta_1) < d(\theta^*, \theta_2)\) 일 때 $L(y, f_{\theta_1}(x)) > L(y, f_{\theta_2}(x))$ 이럴 경우는 절대 없는거? 아닐꺼같은데…
• 뭔가 머리속에서 Loss function이 어떤 특징을 지니냐에 따라 convex가 성립하냐 안하냐 달릴꺼같은데, 이건 수학이 너무 빡쌜꺼같음.

SGD 까지는 직관적으로 이해가 되었지만, 그 이후 모멘텀이 등장한 이후로 학부 때 제대로 이해 못하고 그런갑다 하고 넘어갔었다.

1. Momentum (1980s–1990s 전통 최적화에서 도입)

찾아보니 굉장이 유서 깊은 방식이었다. 핵심은 residual 느낌으로 이전 스텝에서 가고있던 방향에 현재 스텝에 구한 방향을 한스푼 첨가하는 방식이었다.

근데 살짝 헷갈렸던게 Loss 구할 때 내부에서 여태까지 계산된 모든 history (computational graph)가 같이 저장되는데 $v$도 그 그래프 내역이 저장되어있는건지 의문이 들었다. 그런데 $v_t$는 과거 gradient들의 가중 평균 state로 상수 역할을 한다고 한다.
보통 $\beta$는 0.9를 둔다. 즉, 이전방향 0.9배에다가 현재 SGD로 구한 방향 0.1을 더해서 방향이 일정하면 가속이 계속 붙어서 모멘텀이라는 이름이 붙여졌다.

일단 $v$ 가지고 있어야하니 VRAM 2배로 먹음

2. Nesterov Accelerated Gradient (NAG, 2000s)

얘는 너 어차피 그쪽 방향으로 $\beta$배 만큼 갈꺼잖아. 걍 거기서 gradient 계산해라. 이런 느낌이다.
Momentum 방식이 loss surface가 valley 많은 곳에서 모멘텀 때문에 최적점을 지나쳐 튕겨나가는 케이스가 많이 존재한다고 한다.

• 먼저 쎄게 밀고 나중에 gradient 계산 -> 내릴곳 지남…

Nesterov는 밀기 전에, 미리 밀린 위치에서 gradient를 보고 나서 업데이트하자는 얘기다. 그러면 적어도 튕겨나가지는 않을 테니까.

3. AdaGrad (2011)

기본 Gradient Descent는 모든 파라미터에 같은 learning rate를 씀

문제

1. 어떤 파라미터는 gradient가 자주 크게 나옴
2. 어떤 파라미터는 gradient가 거의 0에 가까움

특히 sparse 데이터(NLP, word embedding) 에서 문제 심각

• 자주 등장하는 feature → gradient 자주 큼
• 드물게 등장하는 feature → gradient 거의 없음

이 둘에 같은 learning rate 쓰면 너무 비효율적임.

여기서 핵심 아이디어는 각 파라미터가 과거에 얼마나 gradient를 많이 받아왔는지를 가지고 있는것.

파라미터별로 따로 저장됨. 즉, weight 하나마다 자기만의 G가 있음.

그래서 파라미터 업데이터에 자주 활용된 놈일수록 패널티가 많이 들어가버린다.

4. RMSProp (2012, Hinton) 힌튼햄 입갤ㄷㄷ;

AdaGrad의 핵심 아이디어는 “파라미터마다 과거 gradient 크기를 누적해서 learning rate를 조절하자”였지만,

치명적인 문제 하나가 있음. \(G_t = \sum_{i=1}^{t} g_i^2\)

이 값이 계속 누적되기만 해서 끝없이 커짐. 그러면 learning rate가 다음처럼 점점 0에 가까워져 버린다 (너무 자주쓰인다고 아예 못쓰게함ㅋ)

$\frac{1}{\sqrt{G_t}} \to 0$

훈련 중반부터 파라미터가 거의 안 움직여버리는 현상이 발생하는데 이게 AdaGrad가 초반에는 빠른데 금방 멈추는 이유임.
힌튼햄은 이거를 EMA로 해결해버림.

• $g^2$ 을 그냥 계속 더하지 말고, 오래된 것은 점점 잊고, 최근 것에 더 가중치를 주자.

• $ \rho:$ 보통 0.9

Momentum 처럼 자주 활용되는 파라미터놈을 EMA로 처리해준다.

5. Adam (2015)

Momentum + RMSProp를 합친 구조다.

• 1차 모멘텀 $m_t$: gradient의 EMA → (방향 + 관성)
• 2차 모멘텀 $s_t$: gradient²의 EMA → (파라미터 업데이트 강도 조절)

SGD -> momentum -> RMS 이렇게 순차적으로 보니까 이제 이해가 됨.

보통 $\beta_1 = 0.9, \beta_2 = 0.999$ 을 둔다.

파라미터 업데이트

근데 여기서 사실 이렇게 업데이트 하지않고 어려운 부분이 등장함. $m_t, s_t$ 를 곧바로 쓰지 않고

이렇게 한스텝 꼬아주는데, 이부분에서 좀 막혔음.
문제의 출발점은 $m_0 = 0, s_0 = 0$ 으로 시작할 때 발생함.
초기 $m_t$ 를 살펴보면

• $m_1 = 0.1 g_1$ (원래 gradient의 10%)
• $m_2 = 0.9 m_1 + 0.1 g_2$ (저장된 gradient의 9% + 원래 그래디언트의 10%)

초기 몇 스텝 동안 $m_t$는 실제 gradient 평균보다 훨씬 작은 값이고, $s_t$는 $β_2 = 0.999$ 라 더 심각함.

• m_t 작음
• $s_t$ 더 작음 → $\sqrt{s_t}$ 더더 작음
• 너무 작아져서 update 폭이 지나치게 커질 수 있음 즉,
• $m_t$는 너무 작아서 “방향” 정보 약해짐
• $s_t$는 더 작아서 lr가 미쳐 날뛸 수 있음

초기에는 EMA가 불안정하게 학습을 유도해버림. 이 원인은 바로 $m_0, s_0$ 을 0으로 박아놓으면서 생긴 문제임.
우리가 차트를 볼 때도 지수평균 5일선, 20일선 등등 시작 가격 ~ 오늘가격에서 계산하을지 초기값을 0원으로 박아놓고 시작은 하지 않는다.

• 물론 학습에서는 첫 gradient 방향, 첫 파라미터 스케일을 알 수 없기에 0으로 놓아야하지만…

그렇기에 이 Bias를 보정해주어여하며, 이거는 원래 통계할 때 EMA파트에서 배웠던 거였다 (다 까먹음ㅋ).

초기값이 0이라서 EMA가 평균을 내기 아니라 “0에서 서서히 탈출하려고 애쓰는 값”이 되어버림.

자고로 평균이란, 가중치들의 합이 1이 되어야하는데 EMA 에서는 $(1-\beta)(1 + \beta + \beta^2 + \cdots) = 1$ 무한하게 해야만 1이 된다. 애초에 실전 EMA 케이스는 가중치 합이 1이되는 평균을 줄 수 없을 뿐더러, 초기값까지 0으로 박아버리면 초반 평균이 매우 bias한 상태가 되어버린다.
스텝이 쌓이다면 모를까, 초반에는 bias한 평균이 구해지는데 학습 상황에서 초반스텝이 박살나 버리면 학습이 이상하게 되므로 unbias한 EMA를 이용해 주어야 그나마 안정적인 학습이 가능해짐.

그렇다면 여기서 가중치 부분만 때어와서 보자.

• 등비수열 공식: $1 + \beta_1 + \beta_1^2 + \dots + \beta_1^{t-1} = \frac{1 - \beta_1^t}{1 - \beta_1}$

따라서 (학습 상황에서), $t$ 스텝에서 적용되는 EMA 가중 합은 아래와 같음.

• $m_0 = 0, \beta_1 = 0.9$
• $m_1 = \beta_1 m_{0} + (1 - \beta_1)\, g_1$ 의 가중합: 0.1
• $m_2 = \beta_1 m_{1} + (1 - \beta_1)\, g_2$ 의 가중합: 0.19
• $m_3 = \beta_1 m_{2} + (1 - \beta_1)\, g_2$ 의 가중합: 0.65

스텝이 쌓일수록 bias 가중합 $1 - \beta_1^t$이 1에 가까워져 안정적이 되지만, 초반부는 개박살이 나는것을 확인할 수 있음.
따라서 unbias 가중합을 적용한 EMA를 적용시키기 위해 $m_t, s_t$에다가 한스텝을 주는 것.

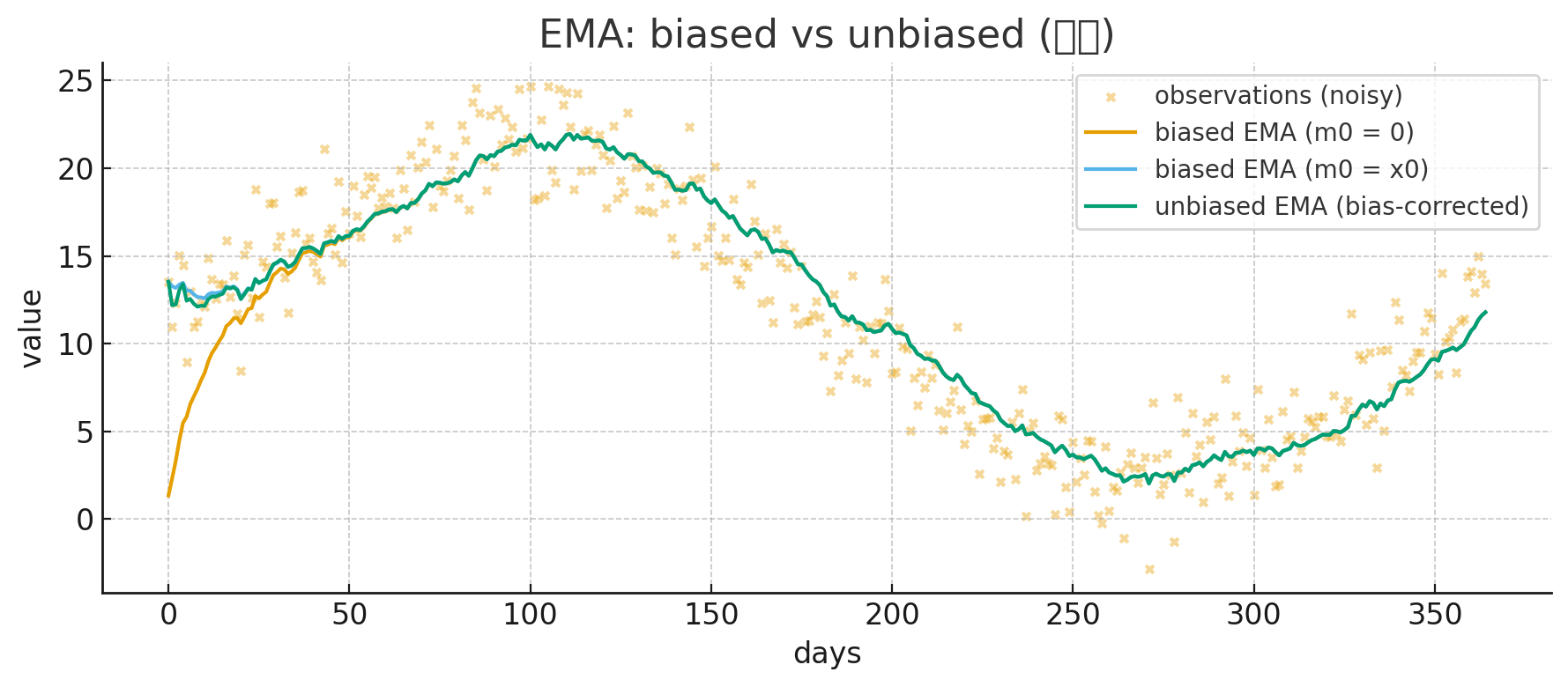요약하면 애초에 EMA 실전에서 쓰기에 가중합 1이 안되서 불안정한데, 여기에 초반 모멘텀, 가중치 강도 0으로 주니까 더 심해져 버림. 그래서 unbias 가중치 주려고 $\hat{m}_t, \hat{s}_t$를 쓴다.

6. AdamW (2017)

AdamW는 Adam의 weight decay 구현이 잘못되어 있었다는 문제를 바로잡은 버전.
현대 딥러닝(Transformer, Diffusion 등)에서는 Adam 대신 AdamW가 사실상 표준 (근데 VRAM 존나 잡아먹음, 파라미터 x3배).
까먹고 있던 weight decay 개념이 등장해서 잠깐 당황했음. 파라미터 업뎃할 때 loss를 줄일 수 있는 방향인 gradient와 더불어 weight가 너무 커지지 않도록 고삐를 잡아주는 weight decay ($L_2$)가 디폴트로 포함된다.

여기서 보면 정규화텀이

• $\hat{m}_t$에도 들어감
• $t{s}_t$ (RMSProp 역할)에도 들어감

weight decay가 “gradient scaling”의 영향을 받아버리는 문제가 발생함. -> 즉, 정규화 효과가 제대로 안 나온다.
해결방법: weight decay 따로 빼서 adam 계산 후 정규화 텀 추가해줌 ㅋ

기존 파라미터 업데이트방식

• gradient 업데이트 + weight decay가 한 수식 안에서 섞여서 적용됨

AdamW 업데이트 방식

• “gradient 기반 업데이트(Adam)”를 먼저 하고, 그 다음에 weight decay(L2)를 적용.

최신 기법 (AdamW8bit, Adafactor, Lion, Prodigy)

AdamW8bit

AdamW의 상태값(momentum $m_t$, variance $s_t$)을 32-bit(float32)가 아니라 8-bit로 압축해 저장하는 Optimizer

→ 1/4 VRAM 상태 유지
→ 전체 optimizer 메모리 3× → 1.75× 정도로 감소

저장만 8-bit quantization으로 하고 계산 필요할 땐 32-bit으로 다시 바꿔서 하고 반복한다.

• 일반 AdamW와 거의 동일한 성능
• LoRA, QLoRA, DreamBooth, Diffusion finetuning 등에서 표준
• 델일수록 효과가 큼
• Full precision AdamW 대비 손실 없는 optimizer

import bitsandbytes as bnb

optimizer = bnb.optim.AdamW8bit(
    model.parameters(),
    lr=1e-4,
    betas=(0.9, 0.999), # 모멘텀, RMSProp 순서
    weight_decay=0.01
)

Adafactor (T5 학습에 채택됨)

kohya-ss 햄이 주로 default로 박아두던 (SDXL, SD3 학습 때) 옵티마이저로, RTX 4090에서 모델 fp16으로 SDXL 학습 가능하게 함.
Adafactor = “Adam의 2차 모멘텀을 압축한 Optimizer”이다.
Adam은 $m_t$와 $s_t$ 두개를 동시에 가지고 있어야하는데, 파라미터 크기가 N이면 optimizer 상태도 2N (또는 3N) 수준이 필요함.

• 1B 파라미터 모델이면 Adam state만 4~8GB 메모리가 들어가버림 (FLUX가 아마 12B일꺼임)

2차 모멘텀을 “행/열 factorization”으로 저장

Adam의 $s_t$는 가중치(m×n) 전체를 저장.
Adafactor는 $s_t \approx r_t \cdot c_t^T$를 연산을 통해 구함.

• 행 평균 $r_t ∈ (m)$
• 열 평균 $c_t ∈ (n)$

1차 모멘텀($m_t$) 자체를 없앰

1차 모멘텀 state = 0 메모리, 대신 gradient 자체를 scale해서 momentum-like 효과를 냄.

Learning rate도 파라미터 크기에 따라 자동 조절

큰 모델에서 안정적으로 작동.

종합 장/단점.

장점

• 메모리 사용량이 AdamW 대비 수십~수백 배 줄어듬
• 성능이 AdamW와 거의 비슷
• 메모리 = 파라미터 크기의 약 1.5배 수준 (adamW는 거의 3배)

단점

• AdamW보다 안정성이 살짝 떨어질 때 있음
• 작은 모델에서는 AdamW가 더 나음
• 세팅이 많고 잘못 세팅하면 발산 가능 (특히 lr, 경험해봄)
• 최근에는 LLM 파인튜닝에서는 AdamW8bit가 더 대세

요약

• pretraining(대규모 학습) → Adafactor
• finetuning(스몰 배치) → AdamW / AdamW8bit

from transformers import Adafactor
import torch

model = MyModel().cuda()

optimizer = Adafactor(
    model.parameters(),
    lr=None,              # 이게 핵심! relative_step=True면 lr=None
    scale_parameter=True, # 파라미터 크기에 따라 자동 스케일, max(eps, RMS(w_t))
    relative_step=True,   # step에 따라 lr 자동 감쇠(decay) + warmup
    warmup_init=True      # 초반 warmup 자동 적용
)

for step, batch in enumerate(dataloader):
    optimizer.zero_grad()

    outputs = model(batch["inputs"].cuda())
    loss = loss_fn(outputs, batch["labels"].cuda())

    loss.backward()
    optimizer.step()      # 이것만 하면 됨 (scheduler 필요 없음)

Lion Optimizer

Lion 은 2023년에 나온 새로운 1차 모멘텀 기반 optimizer로, AdamW보다 더 간단하고, 더 빠르고, 메모리도 적게 쓰고, 성능도 더 좋은 최신 Optimizer다.
LLM, Diffusion, Vision Transformer 등에서 AdamW를 거의 대체할 수준으로 평가받고 있다고 하는데… 쓰는건 못봄ㅋ;
이건…논문을 봐야 이해하겠는데 너무 비현실적이라 잘 안와닿음. Adam은 1, 2차 모멘텀을 유지하지만 얘는 2차를 버림 (adafactor와 반대). 그리고 모멘텀을 부호로 바꿔서 그걸로 업데이트함.

Adam 업데이트 방식

Lion 업데이트 방식

여기서 중요한 특징:

• gradient의 크기(magnitude)는 무시하고
• 방향(sign)만 사용해서 업데이트

학습 방향만 정확하면 굳이 크기까지 정교하게 따라갈 필요 없다 (개씹상남자식 직진ㄷㄷ)

장점

• 메모리 효율이 좋음
• 연산량이 적고 빠름
• 성능: AdamW와 비슷하거나 더 좋음
  • ViT, ImageNet, GPT/언어 모델, 일부 diffusion/텍스트-이미지 모델에서 AdamW 대비 동급 혹은 더 나은 성능 보고.
• 대형 모델·대형 batch에서 특히 강함

단점

• 상대적으로 새롭고 이론·실무 경험이 적음 (23년식)
• 하이퍼파라미터 스케일이 AdamW와 다름
  • AdamW에서 쓰던 lr → Lion에서는 3–10배 줄이기
  • AdamW에서 쓰던 weight decay → Lion에서는 3–10배 키우기
• 작은 batch / 매우 noisy 환경에서는 불안정할 수 있음
• 프레임워크 최적화는 아직 진행 중

from lion_pytorch import Lion
optimizer = Lion(
    model.parameters(),
    lr=1e-4,          # AdamW 쓰던 lr보다 3~10배 정도 작게 시작 추천
    betas=(0.9, 0.99),
    weight_decay=0.02 # AdamW에서 0.01 썼다면 Lion에서는 좀 더 크게
)

2차 모멘텀도 없는데 $\beta_2$ 있는 이유: 저장용/업데이트용 모멘텀 따로 있음.

Prodigy Optimizer

이새기 공부하려고 여기까지 돌아왔음.
LoRA 기준으로 rank, alpha, 붙이는 부위, 가중치 초기화에 따라 lr이 다 달라짐. 특히 LoRA에 kaming 초기화 해주면 lr이 너무 커져서 기존 모델 능력을 아예 박살 내버림.

따라서 lr이 업데이트 되고, 멈추는 의미를 알아야함.

Prodigy: “학습률을 사람이 정하지 않아도, 모델 스스로 lr의 크기를 추정해서 알아서 적절하게 쓴다.”

Adam의 특징

• Adam은 “gradient의 기울기 모양”만 보고 lr 스케일 조절
• 하지만 “문제가 얼마나 어려운지(스케일)”은 모름
• 그래서 사람이 lr=1e-3, 2e-4, 1e-4 이런걸 맞춰줘야 함

Prodigy의 특징

• 파라미터가 최적에서 얼마나 멀리 있는지를 매 스텝 추정해서 적절한 lr을 자동으로 조절
• lr을 세팅해줄 필요가 거의 없음

최적까지 거리 추정은 gradient의 크기 변화를 보고 D라는 “최적해까지 거리”를 추정한 뒤, D로 learning rate scaling 한다고 함.

Adam과 비슷한데 $d_k, r_k$ 가 추가됨. 이는 현재 파라미터와 최적 파라미터 사이의 거리 추정값으로 이걸로 lr 스케일을 자동 조절해준다.

• $m_k$: Adam의 1차 모멘텀 (gradient 평활화)
• $v_k$: Adam의 2차 모멘텀 (grad² 평활화, RMS scaling)
• $d_k$: 현재 최적해까지의 “거리(scale)” 추정값 → lr 자동 조절 핵심
• $r_k, s_k$: $d_k$를 추정하기 위한 보조 통계량 (거리 예측용)

장점

• lr 거의 자동 (제일 위 plot 참고)
• AdamW 수준의 성능
• GAN/LoRA/ViT 등 다양한 모델에서 잘 작동
• Diffusers DreamBooth의 공식 추천 optimizer 중 하나

단점

• 아직 실무 커뮤니티 adoption은 Adam/Lion보다 낮음

직접쓰면서 궁금했던 부분

1. $d_t$가 올라가기만 하고 안줄어듬
   • 설계적으로 비감소(max)로 되어 있음 → 안전한 최대 lr 찾기용
2. 설정 따라 $d_t$ 곡선이 다르게 나오는 이유
   • $d_t$는 모델 scale, gradient scale을 반영
   • 초기화, LoRA rank/alpha, target modules 등에 따라 scale이 달라짐
3. $d_t$ 상승 멈추는 순간
   • “이 문제에서 사용할 수 있는 적정 learning rate 스케일 찾음”
   • lr warmup 끝났다는 신호
4. lr이 작게 잡힌 의미
   • 어차피 gradient 크기 자체가 작으니까 좀 더 크게 step 밟아도 폭주하지 않는다
   • LoRA rank가 낮으면 trainable weight 스케일이 극도로 작음, alpha scaling도 작으면 gradient도 작음 -> 이건 큰 lr로 가도 안 터지네, 더 키우자

My 실험 내용 해석

• LoRA weight scale이 작을수록(= rank 낮을수록, normal init일수록, attn-only일수록) gradient가 작아진다.
• Prodigy는 gradient가 작으면 “더 크게 가도 안전하다” 고 판단해서 $d_t$(=lr 스케일)을 급격히 키운다.
• 그래서 LoRA 8/1, normal init, attn-only처럼 trainable weight가 작은 설정에서는 lr 상승이 빠르고 최종 plateau 값도 크다.
• 반대로 rank 큰 LoRA, 전체 LoRA 적용, scale 큰 초기화 같은 설정에서는 gradient가 상대적으로 커서 lr 상승이 느리고 plateau도 낮게 형성된다.