Haribo ML, AI, MATH, Algorithm

[논문리뷰]Generative Adversarial Nets part3

2021-08-14
Haribo
ML  AI  Paper_Review
 

지난 포스트로 GAN 논문 리뷰를 마쳤고 이 포스트는 GAN의 코드를 한번 분석 해보겠다.

Reference

GAN이 워낙 인기가 많다보니 여러 GAN시리즈가 있고 많은 고수들의 코드들이 있지만 Apple ML 개발자인 Erik Linder-Norén의 코드가 가장 하트도 많이받고, 또 다양 시리즈의 GAN 코드 구현한게 정리되어있어서 이사람의 코드를 참고해서 보면 좋을 것이다. 하지만 오늘 리뷰할 코드는 다른사람의 코드인데 오래전에 복붙하고 수정해서 출처를 못남기겠다..

import

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision.utils as utils
import torchvision.datasets as dsets
import torchvision.transforms as transforms

from tqdm.notebook import tqdm 

is_cuda = torch.cuda.is_available()
print('cuda available :', is_cuda)
device = torch.device('cuda' if is_cuda else 'cpu')

Data Load

# standardization code
standardizator = transforms.Compose([
                    transforms.ToTensor(),
                    transforms.Normalize(mean= 0.5,   # 3 for RGB channels이나 실제론 gray scale
                                         std= 0.5)])  # 3 for RGB channels이나 실제론 gray scale

# MNIST dataset
train_data = dsets.MNIST(root='data/', train=True, transform=standardizator, download=True)
test_data  = dsets.MNIST(root='data/', train=False, transform=standardizator, download=True)


batch_size = 200
train_data_loader = torch.utils.data.DataLoader(train_data, batch_size, shuffle=True)
test_data_loader  = torch.utils.data.DataLoader(test_data, batch_size, shuffle=True)

이 부분 데이터가 다운로드가 안되서 예외가 뜰 수 있는데 예외뜬거 그대로 복사해서 구글링하면 해결법 나와있다. 직접 데이터 다운받아서 root 폴더에 넣어주면됨.

시각화

import numpy as np
from matplotlib import pyplot as plt

def imshow(img):
    img = (img+1)/2    
    img = img.squeeze()
    np_img = img.numpy()
    plt.imshow(np_img, cmap='gray')
    plt.show()

def imshow_grid(img):
    img = utils.make_grid(img.cpu().detach())
    img = (img+1)/2
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1,2,0)))
    plt.show()

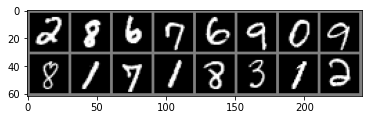
# check MNIST data
example_mini_batch_img, example_mini_batch_label  = next(iter(train_data_loader))
imshow_grid(example_mini_batch_img[0:16,:,:])

img

Generator

# 100 Dimension latent space
d_noise  = 100
d_hidden = 256

height = 28
width = 28

# 평균 0, 분산 1인 정규분포에서 100개의 숫자를 뽑아서 latent vector를 만듬
def sample_z(batch_size = 1, d_noise=100):
  	'''
  	batch_size : 만들 latent vector 개수
  	d_noist : latent space의 dimension
  	'''
    return torch.normal(0, 1, size = (batch_size, d_noise), device=device)

# 2개의 hidden layer를 가진 G MLP model
G = nn.Sequential(
    nn.Linear(d_noise, d_hidden),
    nn.ReLU(),
    nn.Dropout(0.1),
    nn.Linear(d_hidden,d_hidden),
    nn.ReLU(),
    nn.Dropout(0.1),
    nn.Linear(d_hidden, height*width),
  	# input image를 normalize 했기 때문에 tanh로 범위 맞춰줌
    nn.Tanh()
).to(device)

# 노이즈 생성하기
z = sample_z()
# 가짜 이미지 생성하기
img_fake = G(z).view(-1,height,width)
# 이미지 출력하기
imshow(img_fake.squeeze().cpu().detach())

# Batch SIze만큼 노이즈 생성하여 그리드로 출력하기
z = sample_z(batch_size)
img_fake = G(z)
imshow_grid(img_fake)

img

img

Discriminator

# G 와 같은 MLP지만 출력층이 sigmoid
# input의 분포에대한 확률값을 출력한다.
D = nn.Sequential(
    nn.Linear(height*width, d_hidden),
    nn.LeakyReLU(),
    nn.Dropout(0.1),
    nn.Linear(d_hidden, d_hidden),
    nn.LeakyReLU(),
    nn.Dropout(0.1),
    nn.Linear(d_hidden, 1),
    nn.Sigmoid()
).to(device)

print('G(z)\'s shape : ', G(z).shape)
print('D(G(z))\'s shape : ', D(G(z)).shape)
print('가짜 데이터가 p_data에서 왔다고 판단할 확률', D(G(z)[0:5]).transpose(0,1).data)

G(z)'s shape :  torch.Size([200, 784])
D(G(z))'s shape :  torch.Size([200, 1])
가짜 데이터가 p_data에서 왔다고 판단할 확률 tensor([[0.4857, 0.4858, 0.4861, 0.4789, 0.4847]], device='cuda:0')

Trainer

def run_epoch(generator, discriminator, _optimizer_g, _optimizer_d, k):
    for img_batch, label_batch in train_data_loader:
        img_batch, label_batch = img_batch.to(device), label_batch.to(device)

        generator.train()
        discriminator.train()
        
        # Training D first
        # D는 G와 학습 수준을 맞추기 위해 k번 학습
        for _ in range(k) :
            _optimizer_d.zero_grad()

            p_real = discriminator(img_batch.view(-1, height*width))
            # batch_size 만큼 가짜 이미지 생성
            p_fake = discriminator(generator(sample_z(batch_size, d_noise)))

						# V(D, G) while training D
            loss_real = -1 * torch.log(p_real)   
            loss_fake = -1 * torch.log(1. - p_fake) 
            loss_d    = (loss_real + loss_fake).mean()

            loss_d.backward()
            _optimizer_d.step()

        # Training G
        discriminator.eval() # Discriminator은 G가 학습될동안 학습되면 안되기 때문에 eval()로 gradient 계산 금지
        _optimizer_g.zero_grad()
        # batch_size 만큼 가짜 이미지 생성
        p_fake = discriminator(generator(sample_z(batch_size, d_noise)))

        # G의 빠른 학습을 위한 gradient trick
        loss_g = -1 * torch.log(p_fake).mean()

        loss_g.backward()
        _optimizer_g.step()

def evaluate_model(generator, discriminator):
    p_real, p_fake = 0.,0.

    generator.eval()
    discriminator.eval()

    for img_batch, label_batch in test_data_loader:
        img_batch, label_batch = img_batch.to(device), label_batch.to(device)
        with torch.autograd.no_grad():
            p_real += (torch.sum(discriminator(img_batch.view(-1, height*width))).item())/10000.
            p_fake += (torch.sum(discriminator(generator(sample_z(batch_size, d_noise)))).item())/10000.
    # p_real + p_fake != 1
    # 각 데이터에대한 독립적인 확률값임
    return p_real, p_fake

# model parameter 초기화하는 함수
def init_params(model):
    for p in model.parameters():
        if(p.dim() > 1):
            nn.init.xavier_normal_(p)
        else:
            nn.init.uniform_(p, 0.1, 0.2)

Training

criterion = nn.BCELoss()
            
init_params(G)
init_params(D)

optimizer_g = optim.Adam(G.parameters(), lr = 0.0001)
optimizer_d = optim.Adam(D.parameters(), lr = 0.0001)

'''
D가 출력하는 각 데이터들 확률값들의 리스트
'''
p_real_trace = []
p_fake_trace = []

k = 1
for epoch in tqdm(range(200), desc = 'Epoch'):

    run_epoch(G, D, optimizer_g, optimizer_d, k)
    p_real, p_fake = evaluate_model(G,D)

    p_real_trace.append(p_real)
    p_fake_trace.append(p_fake)

    if((epoch+1)% 20 == 0):
        print('(epoch %i/200) p_real: %f, p_g: %f' % (epoch+1, p_real, p_fake))
        imshow_grid(G(sample_z(16)).view(-1, 1, 28, 28))

image-20210815180532569

plt.plot(p_fake_trace, label='D(x_generated)')
plt.plot(p_real_trace, label='D(x_real)')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)

plt.show()

img

둘다 0.5의 확률로 수렴하는것을 볼 수 있는데 이는 사실 잘못되어가고 있는상태로 볼 수 있다. $D$는 input이 real image일 확률을 출력해주는 역할을 해야한다. 가장 이상적인 형태는 $D(x_{real})$의 확률은 1에 가깝고, $D(x_{fake})$는 계속 상승해서 1에 가까워지는 형태가 가장 이상적이다. 논문에서 “$D$ is $\frac{1}{2}$ everywhere” 이라는 부분이 있는데 이는 이론적으로 완벽하게 학습된 GAN은 $D(x_{real}) = D(x_{fake}) = 1$ 이 된다. 따라서 $D$가 정답을 통계적으로 고를 수 없고 찍을 수 밖에 없기 때문에 $D = \frac{1}{2}$이 된다라고 한것이다.

vis_loader = torch.utils.data.DataLoader(test_data, 16, True)
img_vis, label_vis   = next(iter(vis_loader))
imshow_grid(img_vis)

imshow_grid(G(sample_z(16,100)).view(-1, 1, 28, 28))

img

위는 원본 데이터의 이미지, 아래는 generated 이미지

Conclude

k값을 바꿔가며 돌리면 generator가 $1$만 생성하다 어느순간부터 아래의 이미지 처럼 아무것도 생성하지 못하는 mode collapse를 확인할 수 있다. $D$와 $G$의 학습상태 차이가 나서 생기는 일인데 이를 극복한것이 바로 Wasserstein GAN이고 다음에 포스트 할 예정이다.

image-20210815181318130

이전 포스트 [논문리뷰]Generative Adversarial Nets part2

다음 포스트 Stargan: Unified generative adversarial networks for multi-domain image-to-image translation

Comments

Content