• Reference
• Background
• 4. Theoretical Results
  • figure 1
  • Algorithm 1
  • 4.1 Global Optimality of $p_{g} = p_{data}$
    • Proposition 1.
    • proof
    • Theorem 1.
    • proof.
  • 4.2 Convergence of Algorithm 1
    • Proposition 2.
    • proof
• 5. Experiments
  • Generator
  • Discriminator
• 6. Advantages and disadvantages
  • GAN의 단점
  • GAN의 장점
• 7. Conclusions and future work
  • future work
  • Acknowledgments

지난 포스트에서 GAN의 아키텍처부분을 살펴보았고 이번에는 수학적으로 왜 GAN이 잘 동작하는지에대해 증명하는 부분과 실험결과 및 결론에대해서 마무리해보겠다.

Reference

• GAN 논문
• GAN tutorial
• GAN 리뷰 포스트 1
• GAN 리뷰 포스트 2
• 십분딥러닝-GAN
• 배경지식(커널 밀도추정)
• 배경지식(볼츠만 머신)
• GAN 의 한계

Background

지난 포스트 초반부에 잠깐 언급했었던 두 확률분포가 얼마다 다른지를 알 수 있는 측도함수 중 하나인 JSD(Jensen–Shannon divergence)에 대해서 알아보고 넘어가겠다. JSD를 보기 이전에 정보량과 엔트로피에대해 알고 있어야하는데 모르면 여기를 참고하길 바란다.

$D_{JS}(P \parallel Q) = \frac{1}{2}D_{KL}(P \parallel M) + \frac{1}{2}D_{KL}(Q \parallel M),\ where\ M = \frac{P+Q}{2} $

$D_{KL}(P \parallel Q) = \sum_{i}^{n}P(i)\log\frac{P(i)}{Q(i)} = \mathbb{E}_{x\sim p}\left [ \log\frac{P(x)}{Q(x)} \right ]$

• 아래처럼 식을 변형하면 $Q$가 $P$의 엔트로피를 얼마나 잘 보존하는 가를 나타내는 식으로 볼 수 있다.
• \[D_{KL}(P \parallel Q) = \mathbb{E}_{x\sim p}\left [ \log\frac{1}{Q(x)} \right] - \mathbb{E}_{x\sim p}\left [ \log\frac{1}{P(x)} \right ]\]

JSD는 두 Kullback–Leibler divergence(이하 KLD) 의 평균이다. 엔트로피는 정규분포의 평균, 카이제곱 분포의 자유도 처럼 어떤 임의의 확률분포의 모수(parameter)의 역할을 할 수 있는데 KLD는 비교하고자 하는 확률분포($Q$)가 비교대상인 확률분포($P$)의 엔트로피를 얼마나 잘 보존하고 있는지의 척도이다. KLD 는 $[0, \infty ]$ 범위를 가지는데 두 확률분포 $P$와 $Q$가 완전히 같으면 0, 완전히 다르다면 $\infty$ 가 된다. 하지만 식에서 볼 수 있드시 KLD는 대칭이 성립하지 않는다

$D_{KL}(P \parallel Q) \neq D_{KL}(Q \parallel P)$

그래서 KLD에 대칭성을 주기위한 거리측도함수가 바로 JSD이다. JSD는 $[0, 1 ]$ 범위를 가지는데 두 확률분포가 완전히 같으면 0, 완전히 다르면 1이 된다. 이전 포스트에서 GAN은 JSD를 이용해 두 확률분포의 차이를 알아낸다고 했는데 이번 포스트에서 아래의 GAN Loss 식이 사실 JSD를 기반으로한 함수 였다는 것을 증명할 것이다.

\[\underset{G}{min}\ \underset{D}{max}V(D, G) = \mathbb{E}_{x\sim p_{data}(x)}[logD(x)]+\mathbb{E}_{z\sim p_{z}(z)}[log(1-D(G(z)))]\]

4. Theoretical Results

이론적 증명을 하기전에 논문에서 친절하게 GAN 학습과정을 직관적으로 보여주기위해 만든 figure가 있는데 그것부터 먼저 보고 넘어가겠다.

figure 1

검은 점선 : $p_{data}$(원본 데이터의 확률분포)

초록선 : $p_{g}$(가짜 데이터의 확률분포)

파란점선 : $D$의 확률 분포

$Z$ : latent space

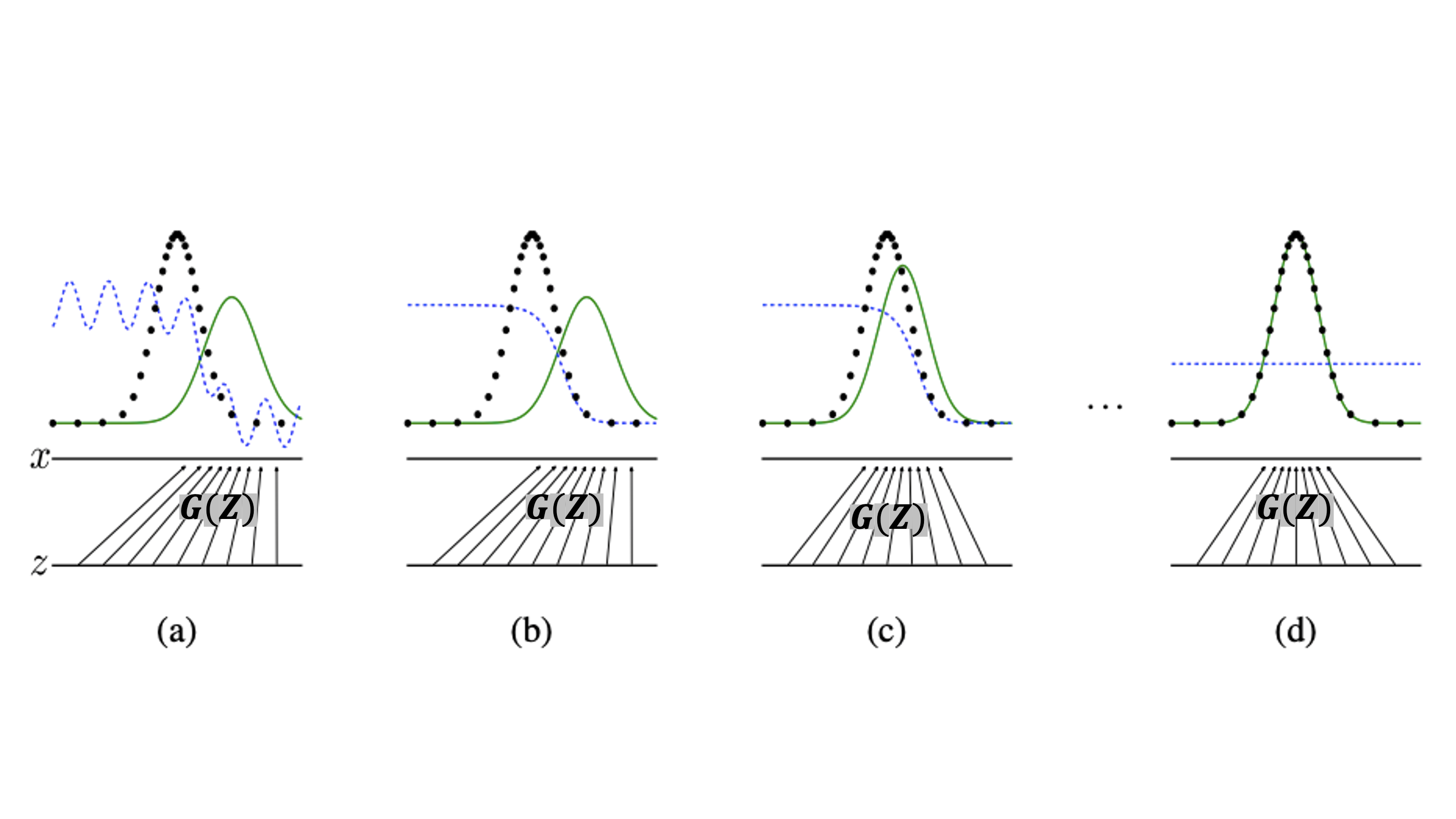
이 figure가 나타내는 것은 a -> b -> c -> d의 시간 순으로 학습이 진행되는 모습을 보여준다. latent space의 변수 $Z$가 $X$ 공간으로 mapping 시켜주는 확률변수 $G$에 의해서 변환된 가짜데이터들의 분포 $p_{g}$(초록선)는 갈수록 원본 데이터의 분포 $p_{data}$에 근사하게 되고, 마지막엔 $p_{data} = p_{g}$가 되어서 $D$는 어떤 데이터가 들어오든 $\frac{1}{2}$ 확률로 진짜와 가짜를 구별하게 된다라는 스토리를 가진 figure다.

• 최종적으로 $D(x_{true}) = D(x_{fake}) = 1$ 이 되어 가짜와 진짜를 구별 못한다는 뜻.

(a) : 초반학습 단계가 지난 뒤, $D$는 완벽하진 않지만 어느정도 제 역할을 해내는 모습이고, $p_{g}$는 어느정도 $p_{data}$에 근사된 모습이다.

(b) : 학습을 통해 $D \rightarrow D^{*}$로 수렴하게됨. $D^{*}(x) = \frac{p_{data}(x)}{p_{data}(x) + p_{g}(x)}$

• $D^{*}$ is optimal $D$

(c) : $D$의 optimal인 $D^{*}$로부터 gradient 값을 받으며 $p_{g}$는 점차 $p_{data}$에 근사하게됨

(d) : $p_{data} = p_{g}$ 가 되어서 $D$가 everywhere에서 $D(x) = \frac{1}{2}$ 이 된 모습

Algorithm 1

본격적으로 증명에 들어간다. Section 4는 Algorithm 1 이 이론적으로 $p_{g}$를 $p_{data}$ 에 수렴(근사)시킬 수 있다는 것을 증명하고자 한다.

• Section 4.1 : minmax game을 기반한 학습이 $p_{g} = p_{data}$로 수렴하는 global optimum 이 존재함을 증명

• Section 4.2 : Algorithm 1이 \(\underset{G}{min}\ \underset{D}{max}V(D, G) = \mathbb{E}_{x\sim p_{data}(x)}[logD(x)]+\mathbb{E}_{z\sim p_{z}(z)}[log(1-D(G(z)))]\)을 최적화 함을 증명

GAN의 Loss 함수를 보면 $D$가 $G$에게 어떤식으로 학습을 해야하는지 gradient를 준다. 즉 $D$ 는 $G$를 지도하는 선생님 역할을 하는 것이다. 이론적으로 완벽한 선생님에게 지도받는 학생은 선생님 만큼 완벽질 수 있다. GAN 논문에서 minmax game이란, 최악의 상황에서 손실을 최소화시키는, 즉 $p_{data}$의 분포를 완벽하게 학습한 $D$가 주는 피드백을 받고 $G$가 학습되는 상황을 말한다. 하지만 이것은 이론적으로나 가능한 일이지 $G$가 학습되기 이전에 $D$는 완벽하게 학습될 수 없다. $D$가 $G$에게 피드백을 주는만큼, $G$도 $D$에게 $p_{g}$에대한 정보를 제공하기 때문이다. 하지만 이 증명은 이론적으로 완벽한 $D$, 즉 $D^{*}$ 가 있다는 가정하에 $p_{g}$는 $p_{data}$에 수렴할 수 있다 라는 것을 증명한다.

4.1 Global Optimality of $p_{g} = p_{data}$

Proposition 1.

Optimal discriminator $D$. 말 그대로 최적의 discriminator를 의미한다. 어떠한 $G$가 오던간에, $G$ 상태가 어떻건 간에 $p_{data}$를 완벽히 학습한 $D$가 있다고 가정한다면 우리는 그 $D$를 $D_{G}^{*}$라고 표기하고 그 값은 $\frac{p_{data}(x)}{p_{data}(x)+p_{g}(x)}$ 가 된다.

\[D_{G}^{*}(x) = \frac{p_{data}(x)}{p_{data}(x)+p_{g}(x)}\]

proof

어떠한 $G$가 오던간에 최적의 $D$를 만드든 일은 $V(G, D)$를 최대화 하는 것이다.

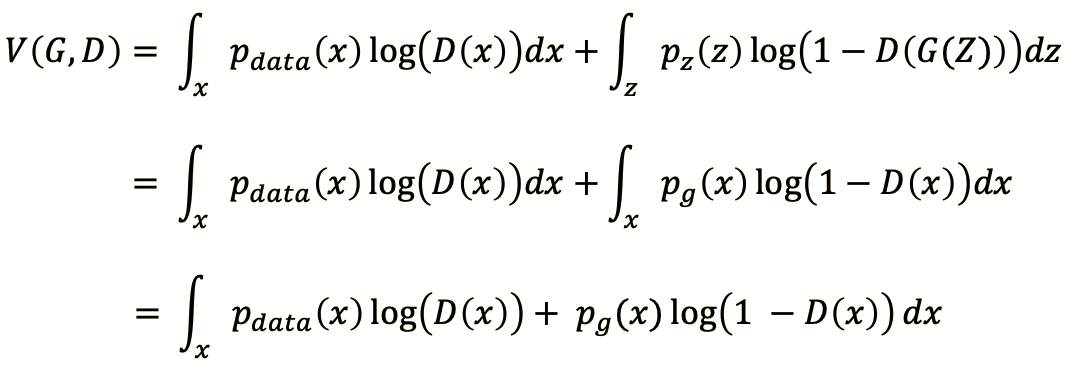
$V(D, G)$ 가 최대가 되기 위해서는 아래의 식이 최대가 되어야하는데 이는 미분을 통해 $V(D, G)$ 가 최대가 되게하는 $D$를 구할 수 있다.

\[\max p_{data}(x)\log(D(x)) + p_{g}(x)\log(1-D(x))\]

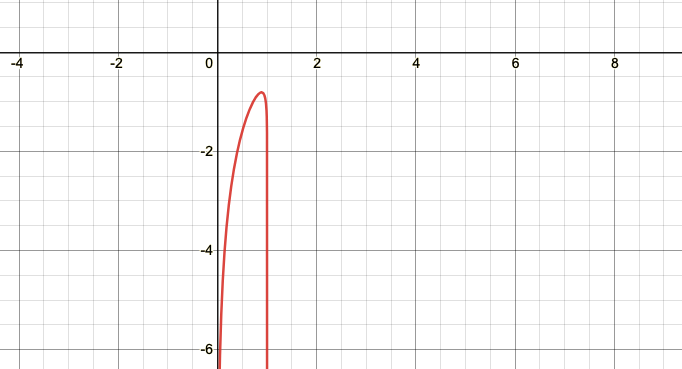
$a, b \geq 0,\ (a, b)\in \mathbb{R}^{2}$ 일 때 $a\log(y)+b\log(1-y)$ 꼴의 식의 그래프는 아래의 그림과 같은 형태로서 최대값이 존재한다. 따라서 미분을 통해 $V(D, G)$가 최대값을 갖게하는 $D$는 \(D_{G}^{*}(x) = \frac{p_{data}(x)}{p_{data}(x)+p_{g}(x)}\)가 됨을 알 수 있다. 그런데 논문에 등장하는 $Supp$ 는 위상수학용어인 지지집합이라고 하는데 나도 위상수학을 몰라서 자세한건 모르겠다. 알고싶다면 여기를 들어가보길 바란다.

그런데 이렇게 $G$를 고정시키고 optimal 한 $D^{*}_{G}$를 대입한 $V(D, G)$는 MLE로 해석할 수 있다. MLE란 주어진 데이터를 바탕으로 그 데이터를 가장 잘 표현하는 확률분포를 찾는 것인데

\[P(Y = y \mid x) \left\{\begin{matrix} y = 1\ if\ x\in p_{data} \\ y = 0\ if\ x \in p_{g} \end{matrix}\right.\]

즉 MLE를 통해 어떤 $x$가 input으로 왔을 때 $p_{data}$ 나 $p_{g}$ 에 따라 다른 확률값을 뱉는 확률분포를 추정하는 것으로 볼 수 있다. 그래서 다시 $V(D, G)$를 재구성 해보자.

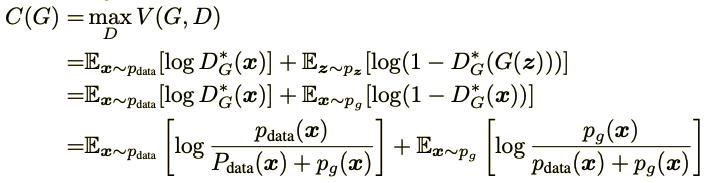
위 식은 임의의 $G$를 고정시켜놓고 최적의 $D$를 대입해서 식을 고친 것이다.

Theorem 1.

$p_{g} = p_{data}$ 일 때 $C(G)$가 최소가 되고 그 때 $C(G)$는 $-\log4$의 값을 가진다.

proof.

논문에서는 주저리주저리 써놨는데 식 유도한번으로 모든게 증명된다.

즉 GAN의 Loss 함수는 $p_{daga}$와 $p_{g}$ 사이의 거리를 줄여나가는 방식으로 학습이 되도록 설계 되었고, 그 거리를 측정하는 방식은 바로 JSD 였던 것이다. $p_{data} = p_{g}$ 인 경우 JSD는 0이 되므로 $C(G)$의 최소값은 $-\log4$가 된다.

4.2 Convergence of Algorithm 1

이 증명은 Algorithm 1이 진짜로 잘 동작하는지 증명하는 내용이다.

Proposition 2.

$D$와 $G$의 성능이 충분하다면 Algorithm 1은 $G$가 주어졌을 때 \(D \rightarrow D^{*}_{G}\) 로 가고 $p_{g}$가 업데이트되면서 $p_{data}$로 수렴하게 된다.

proof

이 부분은 최적화이론을 써서 증명한것같다, 그런데 나는 아무리 봐도 이해가 안되서 해설이 있는 링크를 남긴다. 그래도 대충이나마 해석해 보자면 $D$가 optimal 하다면 $V(D, G)$는 convex함수(왜 convex인지 모르겠음)고 $U(p_{g}, D)$로 표기한다. 그래서 미분이 가능해서 $p_{g}$가 $p_{data}$에 수렴한다 라고한다.

사실 이론적으로는 $p_{g}$를 $p_{data}$에 근사시킬 수 있지만 실제로는 $p_{g}$를 구체화 할 수 없고 가짜데이터를 생성하는 $G(z; \theta_{g})$ 최적화 시킬 수 밖에 없다. 예를 들자면 애가 밖에서 어떻게 할지는 모르니까 가정교육이라도 철저히 시키자, 그러면 이론적으로 밖에서도 잘하겠지 라는정도로 이해해주면 될듯하다.

5. Experiments

실험을 위한 GAN setting

Generator

• mixture of rectifier linear activations
• sigmoid activations

원래는(이 논문에서는) GAN에도 dropout 사용가능하고 layer 중간에 noise를 넣을 수 있지만 실험에서는 input만 noise 사용함. 이유는 안나와있

Discriminator

• maxout activations
• Dropout while training

실험 데이터셋은 MNIST, TFD, CIFAR-10으로 설정하였고 실험결과는 generator가 생성한 가짜데이터들의 확률분포가 test set 데이터들의 확률분포와 얼마나 닮아있는가를 측정하였다. 그 방법은 loglikelihood를 정의하기 힘든 generative 모델들을 성능평가할 때 자주 사용되는 Breuleux의 방법을 사용했다는데 나도 처음보는 거라 자세히는 모르겠다. 대충 보니까 kernel 함수를 이용하는 듯 하다.

그런데 이게 error라면 낮을수록 좋은건데… 결과를 어떻게 해석해야할지 모르겠다. 사실 이 generative 모델을 평가할 좋은 방식이 아직 개발되지 않아서 위의 결과는 좀 신뢰성이 좀 떨어진다고한다. 그리고 GAN으로 생성한 이미지들이 이전 연구들의 결과에비해 더 뛰어난 점은 솔직히 없지만 잠재력은 분명하다라고 한다. 근데 그도 그럴것이 MLP를 기반으로 했으니 성능이 미미한거지 실제로 그 이후에 개발되는 CNN기반으로 한 GAN같은 경우 가짜 이미지를 매우 잘만드는 모습을 보여준다.

6. Advantages and disadvantages

GAN의 단점을 굉장히 재미있게 잘 설명한 블로그가 있어서 링크를 남긴다.

GAN의 단점

1. $p_{g}$ 를 명시적으로 정의하지 않음.

   • 위에서 말했지만 애가 밖에서도 잘 하는지 확인을 하려면 가장 좋은것은 밖에서 생활하는 것을 보고 훈육하면 되지만 실제론 그것이 매우 어렵기 때문에 집안에서 교육을 잘시켜서 밖에서도 잘 생활하길 기대할 수 밖에 없다.
   • 즉 직접적으로 $p_{g}$ 분포를 구해서 $p_{data}$로 근사시키는것이 가장 정확하지만 그렇게 하지 않고 $p_{g}$를 구성하는 가짜데이터를 생성하는 $G$를 학습시킨다.

2. $D$와 $G$의 학습수준이 비슷해야한다.

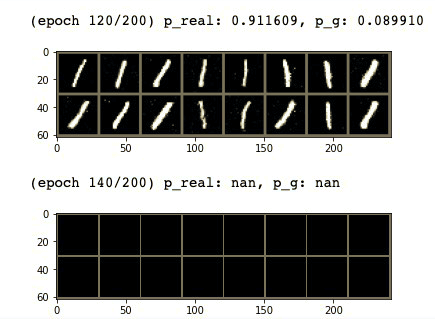
   • 특히 $D$보다 $G$가 더 뛰어나는 경우를 막아야한다는데… 이거는 잘 이해가 안된다. $D$의 학습이 더 쉬워서 보통은 $G$보다 $D$의 성능이 월등히 뛰어날 텐데…실제로도 $D$를 여러번 돌리고 $G$를 한번 돌릴 경우 아래의 그림처럼 Helvetica scenario가 발생하는데. 아무튼 GAN은 $G$와 $D$의 수준차이에 매우 민감하다.

   • 

GAN의 장점

1. 더이상 Markov cahin이 필요하지 않고 backpropagation으로 $G$의 training이 가능하다.
2. 다양한 신경망 모델을 $G$로 쓸 수 있다.
3. 계산적 이득
   • 이전 generative 모델들은 input을 복사해서 사용했나보다. GAN은 forward propagation으로만 학습이 가능하니 계산적으로 이득이라고 한다.
4. 더 다양한 분포를 표현할 수 있다고 한다.
   • 당연히 여러 신경망 모델을 쓸 수 있으니 그럴 것같긴 하다. Markov chains 기반 모델들은 blurry한 분포들밖에 표현하지 못한다고 한다.

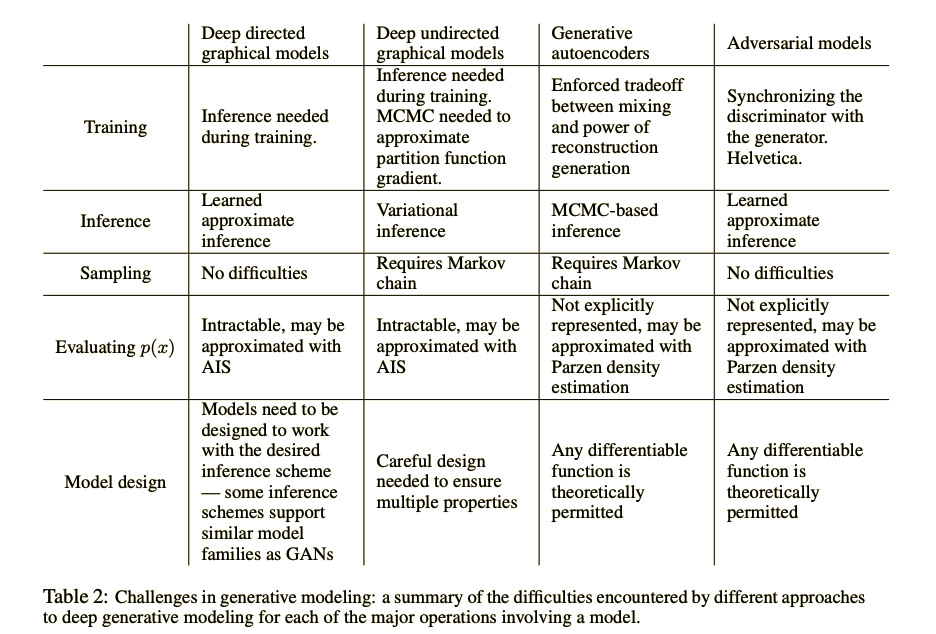
이 table은 GAN과 다른 generative model들의 학습 과정을 detail하게 비교해서 보여주는 표다.

7. Conclusions and future work

[figure 2]

Generator가 sample data를 기반으로 이미지를 생성한 것이 아니라 진짜 학습된 $G$를 기반으로, sample dataset에는 없는, 이미지를 생성한다는 것을 보여주는 예시이다. 가장 오른쪽 열이 가짜데이터와 가장 비슷한 모양을 한 실제 sample data이다. 하여튼 GAN이 가짜를 잘 생성하는 것 뿐만 아니라 sample에 없는 진짜같은 가짜를 생성해낸다는 것을 강조한다.

• (a) : MNIST
• (b) : TFD
• (c) : CIFAR-10 with FC model
• (d) : CIFAR-10 with $D$ is convolutional and $G$ is deconvolutional

[figure 3]

$Z$ 원소를 바꿔가며 변화하는 가짜데이터의 모습을 보여주는 것 같다.

future work

inference net이 뭔지 몰라서 2, 3, 4번은 무엇을 의미하는지 잘 모르겠음. 아마 이전 generative model을 의미하는게 아닐까 싶음.

1. conditional generative model
   • GAN은 원하는 데이터를 생성할 수 없지만 $D$와 $G$에 조건부를 추가해서 원하는 데이터를 생성하도록 할 수 있음.
   • 이거는 실제로 이후에 CGAN으로 연구결과가 발표되었다.
2. sample data로 $z$를 예측하는 모델을 훈련시킴으로서 Learned approximate inference(뭔지모름)을 만들 수 있음.
   • inference net을 학습시키는 wake-sleep algorithm와 비슷하지만 Learned approximate inference은 $G$가 완벽히 학습된 상태에서도 학습 가능하다 라고한다.
3. One can approximately model all conditionals $p(x_{S} \mid x_{\not{S}})$ where $S$ is a subset of the indices of $x$ by training a family of conditional models that share parameters. Essentially, one can use adversarial nets to implement a stochastic extension of the deterministic MP-DBM
   • 이건 도저히 모르겠음
4. Semi-supervised learning
   • Semi-supervised learning(몇개의 데이터는 라벨이 붙어있는 경우)으로 학습하면 $D$ or inference net의 성능을 향상시킬 수 있음.
5. Efficiency improvements
   • $G$와 $D$의 학습 알고리즘을 수정하거나 $Z$의 분포를 개선해서 더 뛰어난 형태의 GAN을 만들 가능성이 충분하다.

Acknowledgments

연구를 도와준 사람들을 샤라웃하는 부분.

이정도하고 끝내려고 했는데 유종의 미는 거둬야하니까 다음 포스트는 GAN 코드리뷰를 해보도록 하겠다.