2014년 Ian. j. Goodfellow에의해 발표된 새로운 방식의 Generative trainning framework 이다. 모델 아키텍처나 코드를 보면 정말 단순하지만 그 원리에관한 이론은 절대로 단순하지 않고 매우 심오하며 어렵다. 3만번이 넘게 인용되었으며 여러 후속시리즈가 계속해서 나오는 매우 근본있고 인기있는 논문임이 틀림없다.
Reference
Background
Generative관련 논문은 이게 처음이라 내가 읽으면서 헤맸던 부분들에대한 배경지식을 먼저 정리하고 논문리뷰를 시작해보겠다. Generative 모델은 인공적으로 데이터(이미지, 음성, 문장 등등)를 생성하는 모델이다. 진짜같은 가짜를 만드는것이 Generative 모델의 궁극적인 목표가 되겠다. 진짜같은 가짜를 만들기위해서는 가짜와 진짜를 비교해서 가짜를 어떻게 발전시켜야하는지를 훈련시에 피드백(Loss function)을 해줘야한다. 그렇다면 가장 중요한 부분은 가짜와 진짜를 구별하는 방법인데 어떻게 해야할까? 우선 가장 쉽게 생각해 볼 수 있는 것은 MSE를 생각해 볼 수 있다.
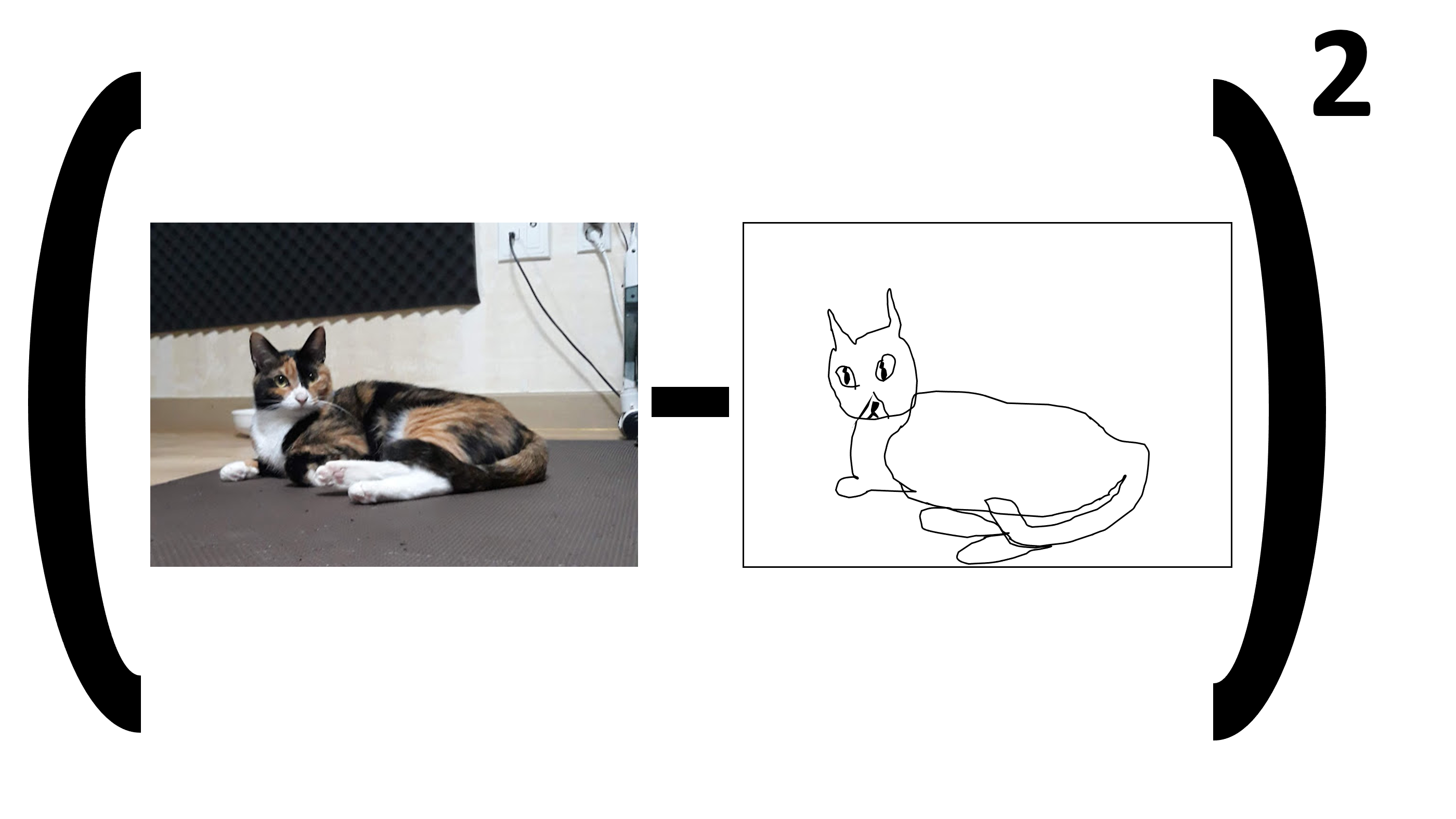
Geneartor가 생성한 가짜이미지와 진짜이미지의 MSE를 Loss 함수로 피드백을 해주면 가장 간단하긴한데 이렇게되면 Generator는 내가 원래 가지고있는 데이터와 비슷한 데이터밖에 생성해내지 못하게된다. 사실 이렇게 MSE로 Loss를 구해서 generator를 학습시켜서 가짜 고양이를 생성할 바에 원래 가지고있는 고양이사진에 noise를 주거나 transformation을 시키는게 나을 것이다. 그렇다면 더 좋은 방법은 generator가 생성하는 데이터의 확률분포가 원본데이터의 확률분포와 비슷하게 생성하게끔 만들어버리는 것이다. 여기서 원본데이터는 이미지인데, 이미지의 확률분포라는 개념이 좀 생소할 수 있지만 확률변수는 scalar값뿐만이 아니고 벡터, 행렬 더 나아가 고차원 tensor 또한 확률변수가 될 수 있다.
확률론에서, 확률 변수(確率變數, 영어: random variable)는 확률 공간에서 다른 가측 공간으로 가는 가측 함수이다
-wikipedia-
나도 이 짧은 문장을 완벽하게 이해하지 못하지만 이 문장의 핵심은 확률변수의 원래정의는 함수이다. 어떠한 확률공간(확률측도)에서 다른 공간(가측 공간)으로 mapping시켜주는 역할을 하는것이 바로 확률변수다.
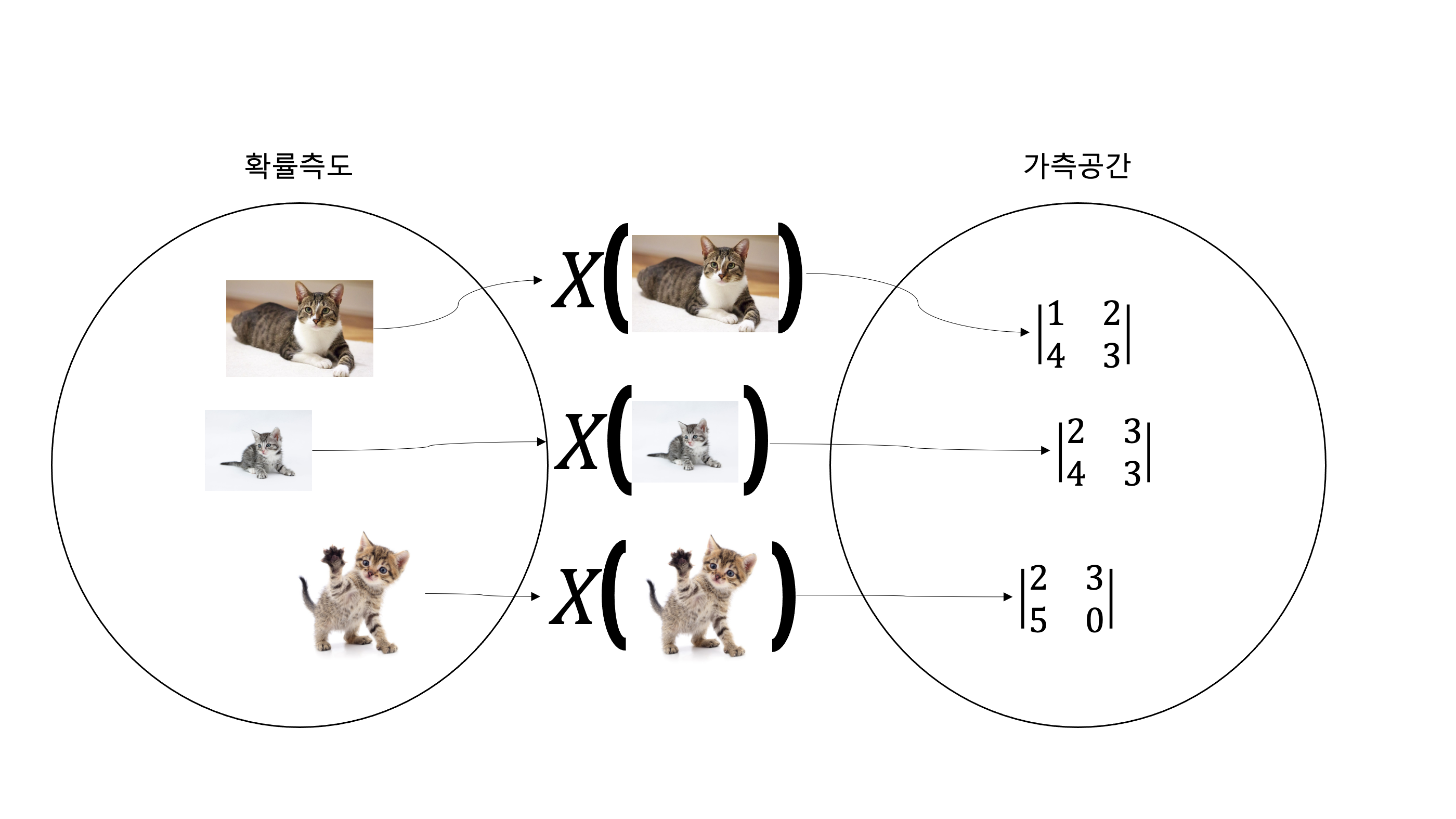
[확률변수]
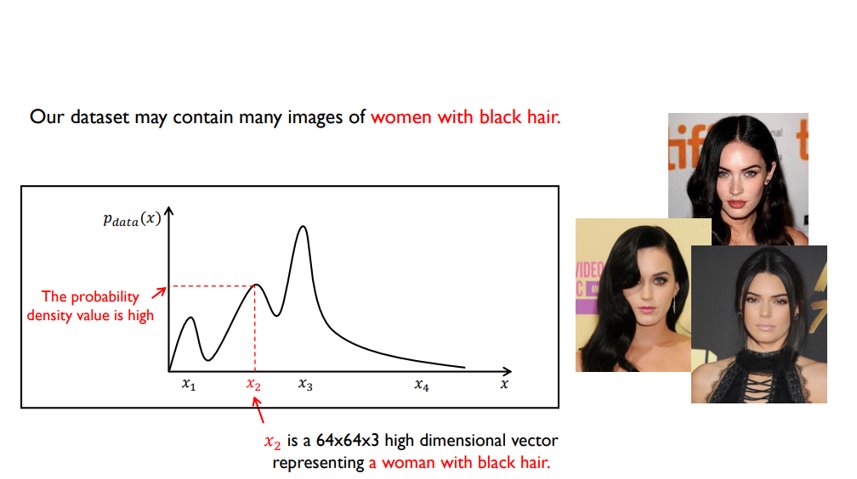
[확률분포]
이렇게 이미지를 특정 행렬 또는 tensor로 mapping시킬 수 있고, 이 확률변수를 $x$축으로한 다차원 확률분포를 생각한다면 이미지의 확률분포의 개념이 그렇게 이상하지는 않을 것이다. 다시 본론으로 돌아와서 원본 데이터의 확률분포를 인공적으로 만든다고 했는데 말을 좀더 우아하게 바꿔서 가짜데이터의 확률분포를 원본데이터의 확률분포로 근사시키는것이 generator의 가장 좋은 방식이라고 할 수 있다. 즉 두 확률분포의 차이(거리)를 알면 그 차이를 줄여나가는 방법으로 가짜데이터의 확률분포를 원본데이터의 확률분포로 근사시킬 수 있게된다. 두 확률분포의 차이를 구하는 방법은 다양하지만 이 논문에서는 Jensen–Shannon divergence (이하 JSD)를 이용했다. JSD에대해서는 section 4의 증명부분에서 자세하게 다루도록하고 이제 본격적으로 논문을 리뷰해보겠다. 리뷰는 원문 해석이아닌 해설형식으로 쓸 예정이며 최소 한번은 이 논문을 읽고 이 글을 보고 다시 논문을 읽는 방향으로 공부하는 것을 추천한다.
0. Abstract
generative model 관련논문은 이것이 처음이기에 이 논문 이전의 generative model들의 트렌드나 상황을 잘 모르지만 예전에는(2014년 기준) generative model은 deep neural network(MLP, CNN 등등)기반이 아닌 통계적 모델(볼츠만 머신, Marcov chain, unrolled approximate inference network)을 기반으로 만들어 졌나보다. 그래서 이 논문 초반부에는 계속 이전 방법들에대한 간략한 소개와 GAN과의 차이점을 설명하는데 굳이 이전 방식들에대한 지식이 없어도(이전 방법들과 GAN의 차이를 이해하지 못해도) GAN자체를 이해하는데에는 문제가 없다(하지만 Generative model 역사를 알고싶다면 꼭 봐야할듯함).
GAN은 두가지 모델을 동시에 학습시킨다.
Discrimicator(이하 $D$) : input 데이터가 원본데이터가 맞는지 확률값을 출력해주는 신경망 모델.
Generator(이하 $G$) : 원본데이터를 모방해 가짜데이터를 생성하는 신경망 모델.
이게 상황이 정말 웃긴게 $G$는 $D$를 속이기위해서 원본 데이터의 분포와 비슷한 데이터를 만들어내도록 노력하는데, $D$는 $G$가 자신을 잘 속이게 만들도록 도움을주면서 $G$가 생성한 데이터와 원본데이터를 구별하려고 노력한다. 마치 자기 자신($D$)을 죽이기위한 암살자($G$)를 자신의 손으로 키우는 상황이다. 이 논문에서는 이러한 상황을 minmax two-player game이라고 한다. minmax game은 “최악의 상황에서 최선의 결과를 내라(기업에서 원하는 인재)” 는 말인데 GAN의 상황에서는 $D$가 강력한 성능을 가졌지만 그래도 $D$를 속이는 데이터를 생성하는 $G$를 학습시키는 상황을 의미한다.
minmax two-player game
최악의 상황 : $D$가 구별을 완벽하게 함
최선의 결과 : 그래도 $D$를 어찌저찌 속이는 데이터를 만드는 $G$를 만들자.
읽다보면 이 부분이 해석이 어려운데
In the space of arbitrary functions $G$ and $D$, a unique solution exists, with $G$ recovering the training data distribution and $D$ equal to $\frac{1}{2}$ everywhere
이 부분은 minmax trainning이 이론적으로 완벽하게 이루어지면 $G$는 원본데이터의 분포와 완전히 같아질것이고, $D$는 $\frac{1}{2}$확률로 가짜와 진짜를 구별할 것이다 라는 행복회로를 돌린부분이다. 그리고 마지막으로 이 논문의 자랑거리 중 하나인 $G$와 $D$는 MLP로 이루어져있어서 backpropagation으로 학습이 가능하다 라는 것을 강조한다.
1. Introduction
여기서는 왜 과서 generative model 연구들이 성공적인 퍼포먼스를 보여주지 못했는지에 대해 설명한다.
Discriminative model
- backpropagation 과 drop 그리고 gradient를 이용한 학습 덕분에 큰 성공을 이룰 수 있었음
Generative model
- MLE를 이용해 원본 데이터의 확률분포를 근사하려 했지만 그것이 매우 어렵고 학습이 어려움
그래서 이 논문은 generative model도 discriminative model처럼 backpropagation, dropout을 사용할 수 있도록 Deep neural network을 기반으로한 generative model을 사용할 수 있게했다 라고 주장한다.
2. Related work
이 부분은 과거의 generative 방식들을 review하면서 GAN은 이들과 어떻게 다른지 그 차이를 설명하는 부분이다. Abstract 에서도 말했지만 이 부분을 읽지 않아도 GAN을 이해하는데 아무런 지장이 없다. 나 또한 과거의 generative model들에 대해 지식이 없으므로 논문에 나온것을 나름 요약해 보겠다. 하지만 안 읽는것을 추천한다.
첫째 문단
과거엔 통계적 접근방식(Markov chain)으로 generative model을 생성했지만, 이러한 방식은 정확한 Loss함수(MLE)를 구할 수 없고 Loss함수를 근사하는 함수를 기반으로 학습이 진행됨 [Boltzman machine]. 이러한 어려움을 극복하고자 MLE를 사용하지 않지만 backpropagation으로 학습가능한 “generative machines” 방식의 generative model들이 나옴[Generative stochastic networks].
[중간에 이 식은 무엇을 의미하는지 모르겠음]
둘째 문단
GAN처럼 backpropagation 기반으로 generative model을 학습 시키는 방법을 고안한 논문이 있는데 이 논문은 VAE를 stochastic backpropagation rule을 통해 학습을 시켰는데 GAN과 다르다(정확히 어떻게 다른건지 모르겠음, 아무튼 다르다고함).
셋째 문단
또 다른 과거 generative modeling 접근 방식은 discriminative criterion을(뭔지모르겠음) 이용했음(Noise-contrastive estimation, NCE). 그런데 NCE 은 GAN과 비슷하게 competition 기반으로 학습시키는데 GAN과의 큰 차이점은 Discriminator 에 있는데 어쩌고 저쩌고 하는데 뭔지 모르겠다. 아무튼 비슷하긴한데 NCE는 Discriminator에 있어서 GAN과 다르다고 한다.
넷째 문단
또 다른 과거 방식 중 2개의 model을 경쟁적으로 학습 시키는 predictability minimization 방법이 있었다고 한다. predictability minimization과 GAN의 가장 큰 차이점 3가지를 설명한다.
- competition between the network is sole training criterion
- nature of the competition is different
- specification of the learning process is different
이 3가지 차이에 대한 각각의 설명을 한다.
다섯째 문단
GAN의 컨셉과 혼동될 수 있는 adversarial examples 에대해 설명한다. adversarial examples는 GAN과 다르고 비효율 적이다…라는 내용이다.
요약하면 GAN은 과거의 generative model의 단점을 보완한 연구가아니라 기존 연구들과 차별된 새로운 연구다 라는것을 강조한다.
3. Adversarial nets
용어정리를 한번 하고 넘어가야한다. 이 부분은 fact 라기보단 이렇게 이해하고 논문을 읽으면 이해하는데 지장이 없다. 그렇다고 막무가내로 헛소리를 써놓은 것은 아니다. 이 논문과 여러 자료들을 읽고 종합한 내 주관적인 정리다.
$p_{data}$ : 원본 데이터의 공간(확률분포)
$p_{g}$ : fake 데이터의 공간(확률분포)
$p_{z}$ : noise 데이터의 공간(확률분포)
$G(z, \theta_{g})$ : $\theta_{g}$를 파라미터로 가지고 $z$를 input으로 받는 함수, 이하 $G$
$D(x, \theta_{d})$ : $\theta_{d}$를 파라미터로 가지고 $x$를 input으로 받는 함수, 이하 $D$
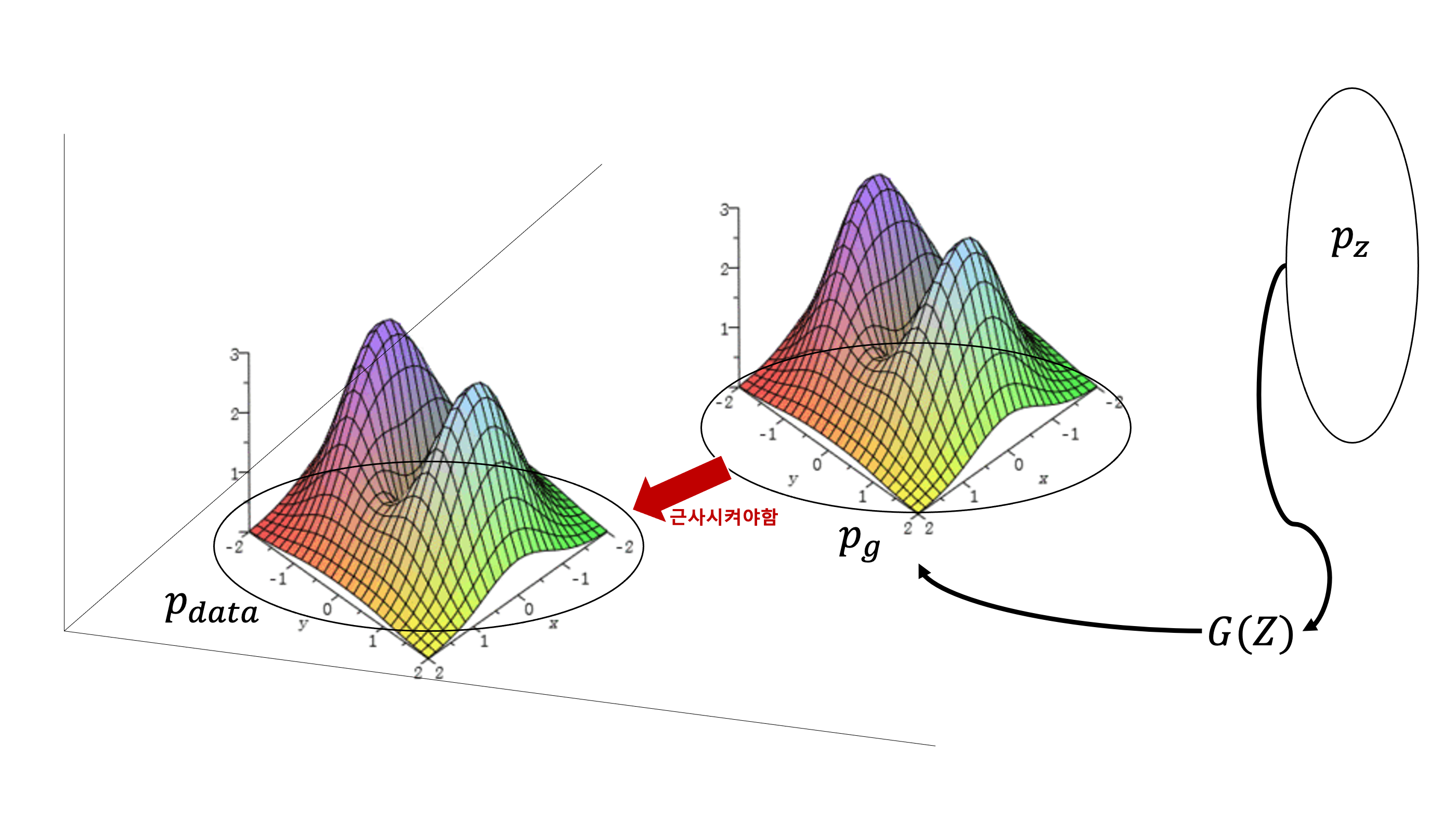
우선 $Z$는 임의의 크기를 가지고 랜던한 숫자들로 구성된 벡터이다. $G$는 $Z$ 공간의 벡터 $Z$를 $p_{g}$로 mapping 시켜주는 확률 변수이고, $D$는 input이 $p_{data}$ 에서 왔을 확률 을 출력해주는 함수이다(진짜 가짜를 구별하는것이 아니라 말 그대로 진짜일 확률을 출력하는 함수임). $D$ 와 $G$ 는 각각 파라미터 $\theta_{d}$, $\theta_{g}$를 가지는 multilayer perceptron이다. 이제 정의된 Loss 함수를살펴보자.
\[\underset{G}{min}\ \underset{D}{max}V(D, G) = \mathbb{E}_{x\sim p_{data}(x)}[logD(x)]+\mathbb{E}_{z\sim p_{z}(z)}[log(1-D(G(z)))]\]
우선 앞에 $min$, $max$ 부분을 제외하고 뒷부분인 $V(D, G)$를 해석해보자.
\(\mathbb{E}_{x\sim p_{data}(x)}[logD(x)]\) : $D$ 가 $x$를 $p_{data}$에서 왔다고 판단할 확률의 기대값
\(\mathbb{E}_{z\sim p_{z}(z)}[log(1-D(G(z)))]\) : $D$가 $G(z)$를 $p_{data}$에서 왔다고 판단하지 않을 확률의 기대값
- $D(G(z)) + D(x) = 1$ 이라는 보장은 없기 때문에 두번째 항을 첫번째 항과 동일한 의미로 생각해서는 안된다. $D$는 classification 모델이 아니다.
$D$는 $p_{data}$(원본 데이터의 확률분포)에 근사하게끔 trainning되는 확률분포함수다. 왜냐하면 $D$는 input이 $p_{data}$의 분포에서 온 데이터라고 판단되면 높은 확률값을, 아니라면 낮은 확률값을 출력해주는 역할을 하기 때문이다.즉 $V(D, G)$는 어떠한 input에 대해 $D$가 출력하는 확률의 기대값에 관한 함수이다.
이제 앞부분을 포함해서 보자
$\underset{D}{max}V(D, G)$ : $V(D, G)$를 최대로 만들도록 $D$를 training
$\underset{G}{min}V(D, G)$ : $V(D, G)$를 최소로 만들도록 $G$를 training
마치 왼쪽을 보면서 동시에 오른쪽을 보는 듯 하지만 이 상황에서 최적의 해가 단 하나 존재한다. $G$가 생성하는 가짜 데이터들의 분포 $p_{g}$ 가 $p_{data}$에 완벽하게 근사하게 되고, $D(X) = \frac{1}{2}$ 가 되는 경우이다. 그래서 section 4에서는 $D$의 성능이 충분할 때 $p_{g}$가 $p_{data}$로 근사할 수 있음을 이론적으로 증명한다. 그리고 GAN은 training 시 $D$를 k번 $G$를 한번씩 번갈아가며 학습을 시켜서 데이터세트가 $D$에 overfitting 되는것을 방지한다.
추가적으로 GAN은 $D$의 성능과 $G$의 성능이 어느정도 얼추 비슷해야 학습이 잘 이루어진다. 이것에 관한 내용은 다음에 포스팅할 예정인 WGAN에서 자세하게 다룰 예정이니 지금은 그냥 ㅇㅋ 하면된다. 그런데 말했듯이 $D$ 와 $G$의 성능이 비슷해야하는데 학습 초반에는 $G$가 생성해내는 가짜 데이터들은 특정 이미지(이 논문에서는 데이터가 이미지임) 형태라기보단 아래 그림처럼 알수없는 noise에 가깝다.

그래서 $D$와 수준을 맞추려면 초반에는 큰 gradient값으로 빠르게 학습이 이루어져야하는데 $V(D, G)$를 그대로 이용하면 학습 초반의 $G$에 대한 gradient가 작아서 $D$와 $G$의 학습 수준이 안맞게되어 학습이 이루어지지 않게된다. 말이 어려우니 그림으로 보자
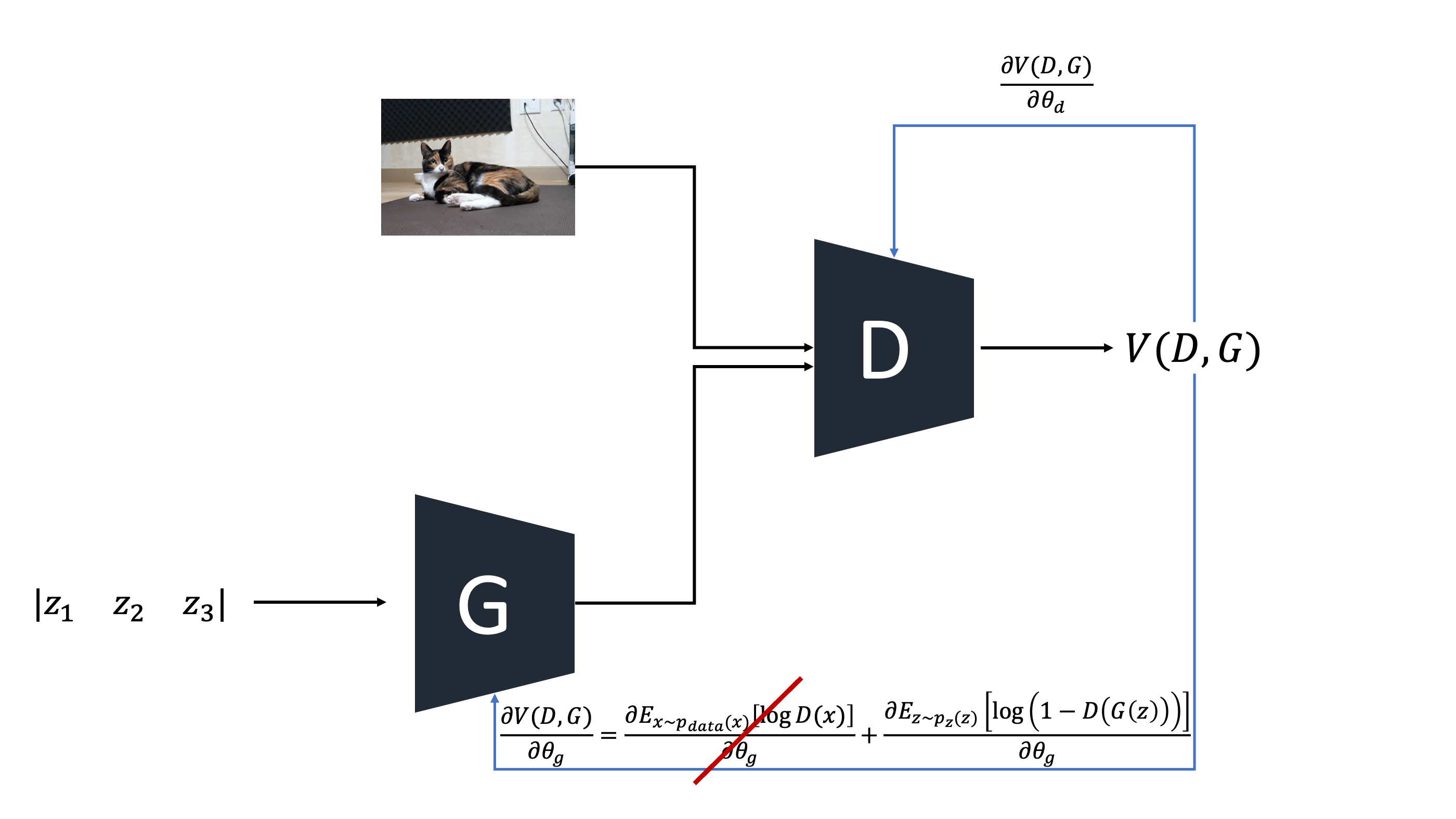
$G$의 역전파 부분만 보면된다. 어차피 $G$의 gradient는 $\theta_{g}$에 대해서 미분할 것이기 때문에 왼쪽 항은 날라가고 오른쪽 항의 기울기를 살펴보면 학습 초기에는 $G$가 생성하는 가짜 이미지가 너무 형편없어서 $D(G(z))$는 거의 0에 가까운 확률값을 출력할것이다. 아래 그림에서 보다시피 그런 경우 gradient의 값이 너무작아서 학습을 하면 할수록 $G$와 $D$ 수준차이가 나게된다.
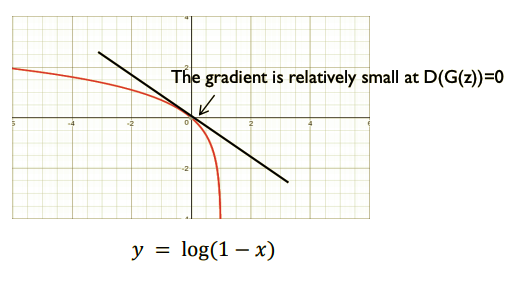
이를 극복하기위해 아래 그림처럼 $G$의 Loss 함수에 trick을 써준다.
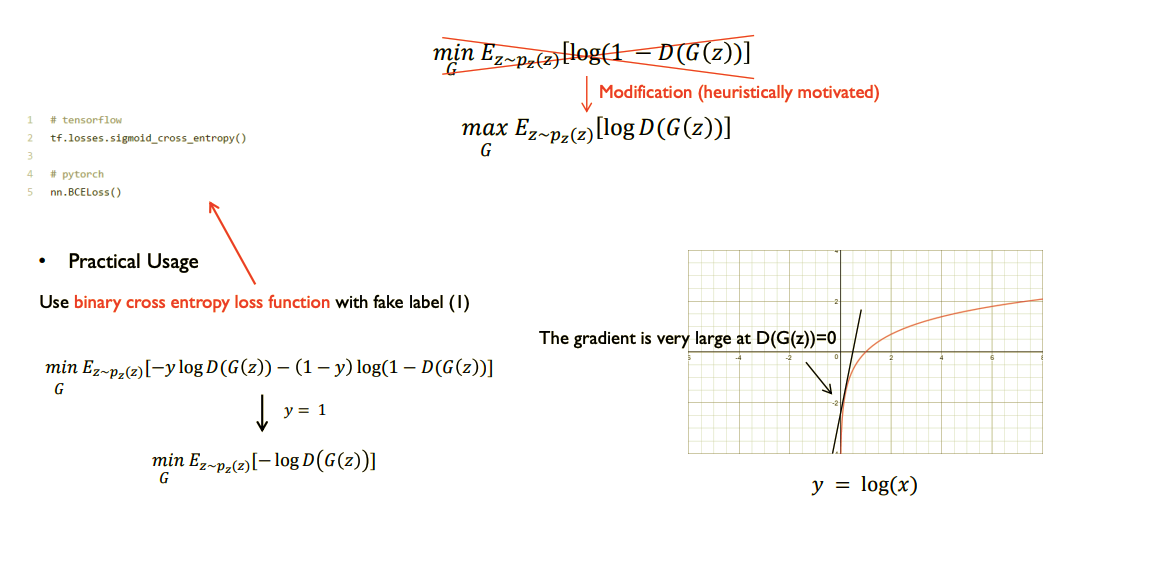
이미지 출처 - 1시간만에 GAN(Generative Adversarial Network) 완전 정복하기
이제 구조적인 부분은 끝났고 다음 포스트에서 Loss 함수에 대한 이론적인 증명부분을 보겠다.