• Reference
• Capsule Network
  • What is Capsule?
  • Dynamic Routing
    • Squash function
  • Loss Function
    • Margin Loss(Supervised Loss Function)
    • Reconstruction Loss(Unsupervised Loss Function)
  • Capsule Network Architecture

지난 post에서는 CNN의 특징과 단점에 대해 정리를 해보았는데 이번 포스트에서는 본격적으로 Capsule Network(이하 CapsNet)에 대해서 정리를 해보도록 하겠다.

Reference

• Dynamic Routing Between Capsules 원본 논문
• 시카고 대학 Dr Charles martin 의 유투브 동영상
• Hands-on Machine Learning 저자 Aurélien Géron 의 유투브 동영상
• 논문 저자 중 한명인 Sara Sabour 의 유투브 동영상
• jayhey’s Blog
• CapsNet 구현코드1 Pytorch 구현
• CapsNet 구현코드2 Pytorch 구현

Capsule Network

내가 CapsNet에 관심을 가지게된 이유가 바로 학교과제 때문에 MNIST ranking을 살펴보는데 성능은 무지막지하게 좋으면서 파라미터수는 엄청나게 적은 모델이 있었다.

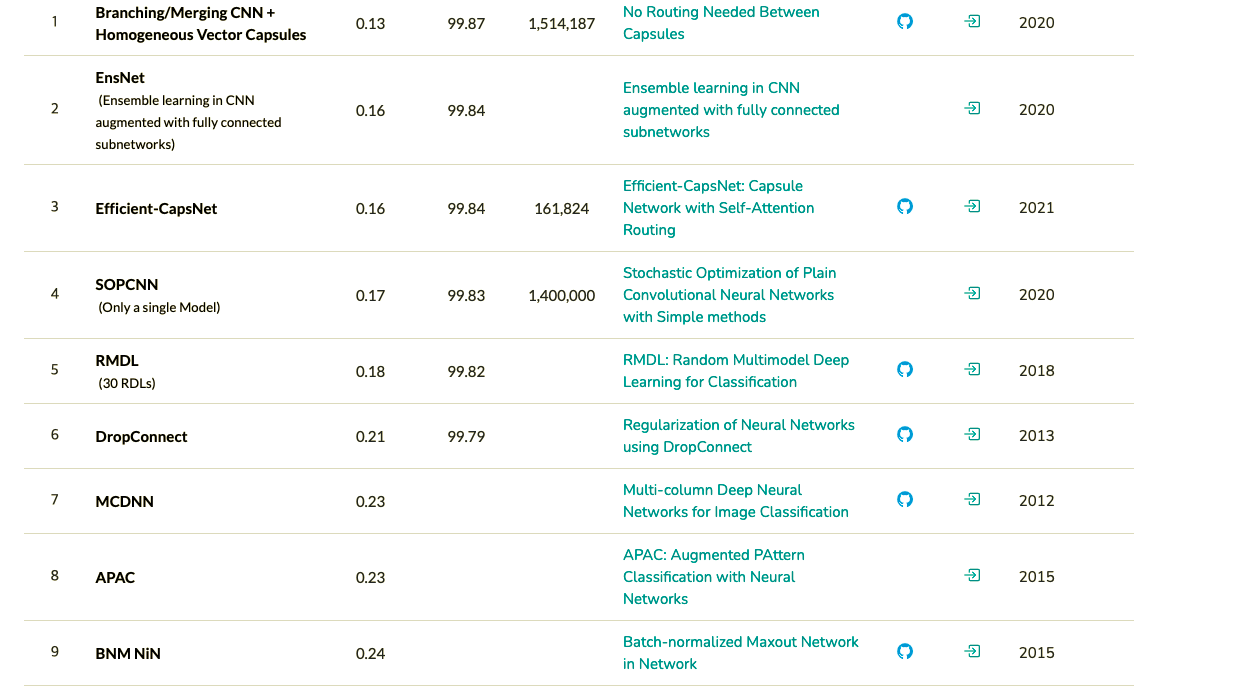
1위에도 Capsule이라는 키워드가 들어가있지만 내가 공부하기로 마음먹었던 이유는 바로 파라미터가 16만개 밖에 필요없는 3위를 기록한 Efficient-CapsNet 이었다. 이 논문을 공부하기 전에 기본적으로 CapsNet에 대해 알아야하기 때문에 CapsNet을 보는데 내가 느낀바로는 CapsNet은 아래의 3가지를 합쳐놓은 모델이다.

• CNN
• DNN
• NLP
  • attention
  • embedding

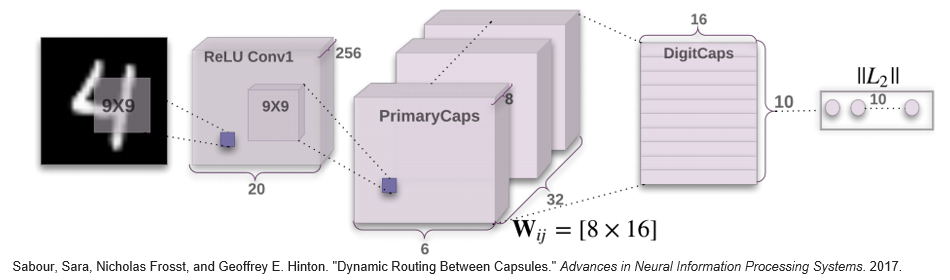
이게바로 논문에 나와있는 CapsNet 모델인데 처음봤다면 뭔소린지 당연히 모를것이다. 지금부터 CapsNet에대한 설명을 시작해 보겠다.

What is Capsule?

CapsNet은 당연하게도 Capsule로 구성된 네트워크이다. 우선 이 Capsule에 대해 설명하기전에 이미지 렌더링과정을 살펴보자.

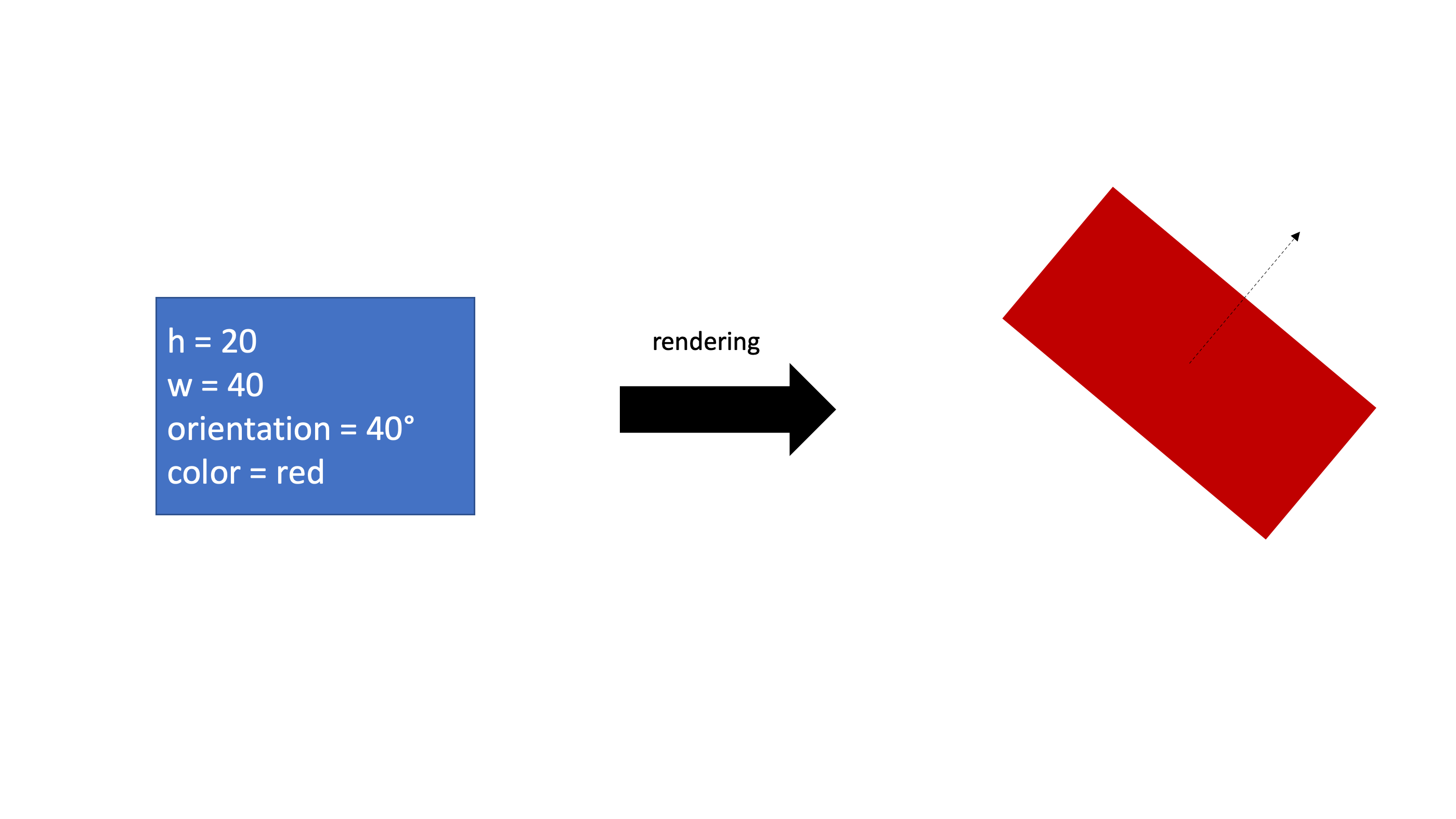
이렇게 표현하고자하는 도형의 정보를 주고 컴퓨터 그래픽으로 구현을 하는 과정을 렌더링이라고한다. 그렇다면 이미지안에서 어떤 entity의 부분 또는 전체를 보고 그 entity의 정보를 벡터형태로 표현할 수 있을 것이고 이를 inverse rendering이라고 한다. 마치 워드임베딩처럼 Capsule이 바로 이미지안의 어떤 entity의 정보를 벡터형태로 표현한 것이다. 그리고 각 entity의 정보들을 의미하는 숫자는 이 논문에서는 instantiation parameter 라고 지칭한다.

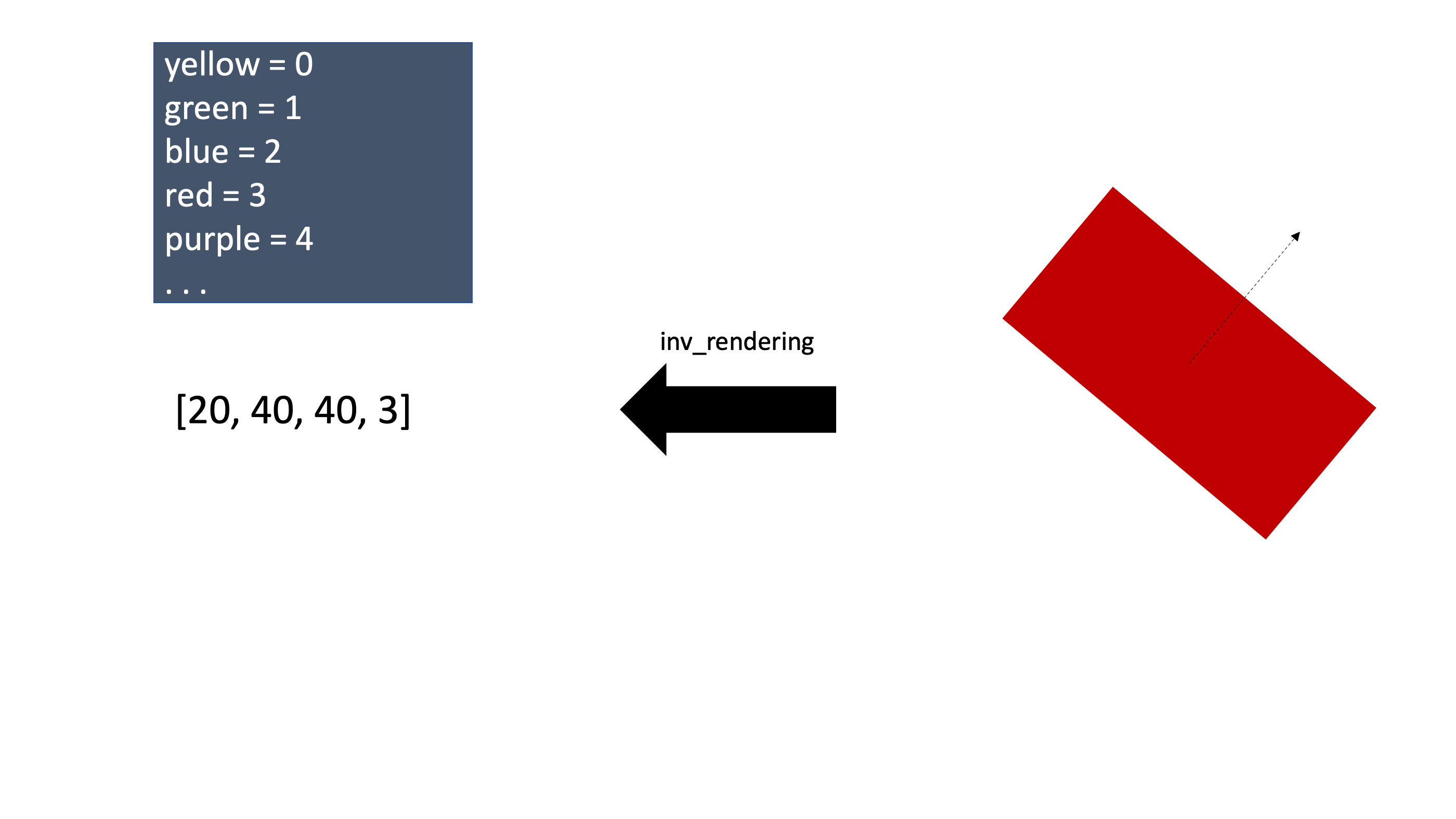
위 이미지의 예시는 사각형 entity를 4차원 벡터로 inverse rendering을 한 모습이다. 당연하게도 워드임베딩처럼 캡슐의 각 instantiation parameter들의 의미는 정하는것이 아니고 학습되는 것이기에 실제로 각 instantiation parameter가 의미하는것이 무엇인지는 알기 어렵다. 위의 예시는 이해하기 쉽도록 임의로 정해준것이다.

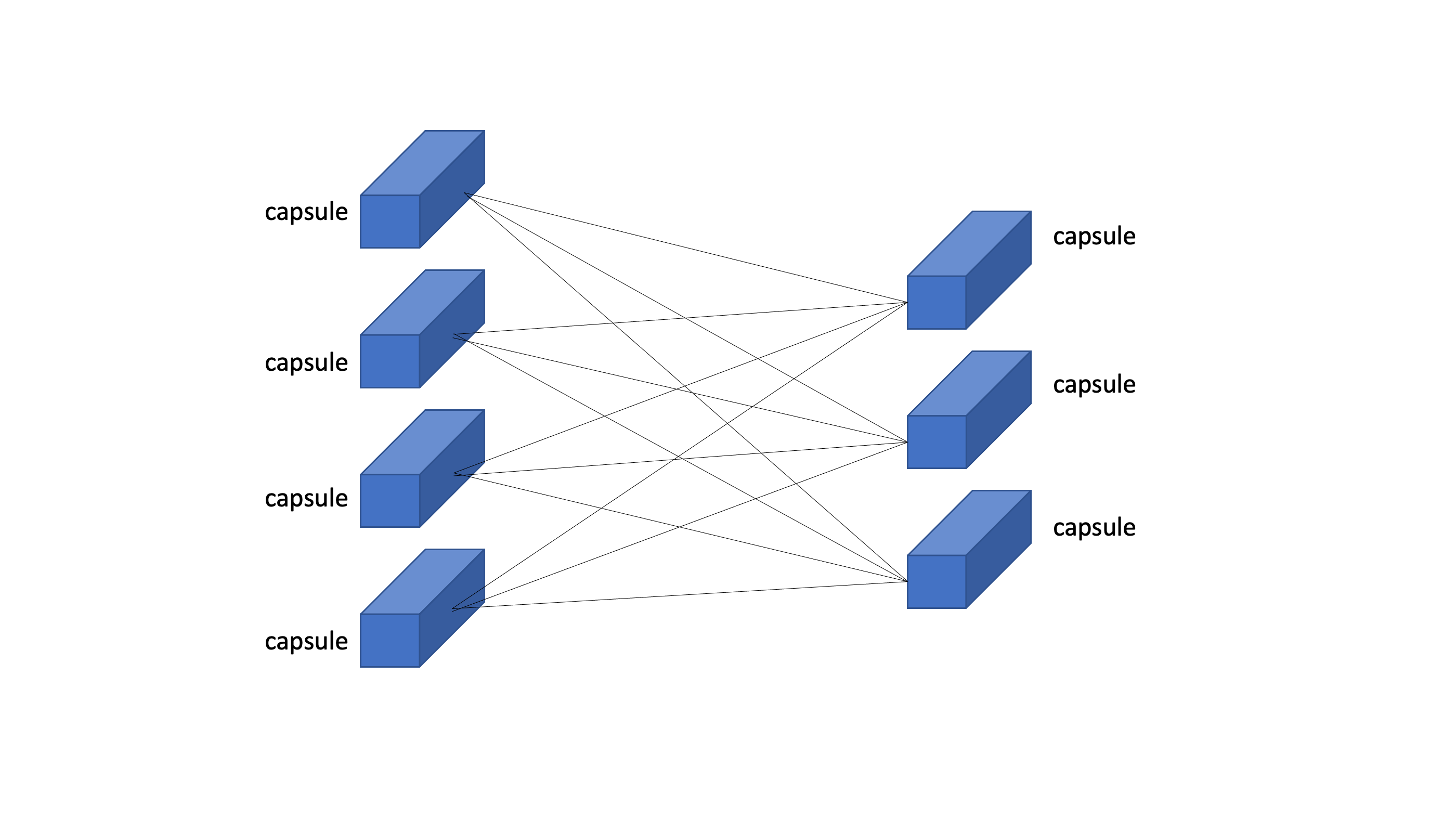
CapsNet은 이렇게 캡슐들이 DNN처럼 구성되어있다. 그리고 이 capsule vector의 길이를 그 entity가 존재할 확률로 쓰고있다. 즉 하나의 capsule은 2가지 정보를 담고있다.

• what is entity? : instantiation parameter
• is there entity? : length of vector

그런데 capsule이 표현하는 entity가 복잡하면 복잡할 수록 이것을 표현하기위해 더 많은 instantiation parameter가 필요하게된다. 잠시 CNN의 feature map을 살펴보자

Low level layer에서는 아주 간단한 특징들만 표현되고, High level layer에서는 low level layer의 feature들을 조합해 더욱 복잡한 특징들이 표현됨을 볼 수 있다. 마찬가지로 CapsNet에서도 이전 capsule들을 조합해 다음 layer에서 더욱 복잡한 entity를 capsule안에 담아야하는데 복잡함을 감당하기 위해 capsule의 차원도 더욱 커져야한다.

이렇게 layer간의 capsule의 차원이 다른데 일반적인 forward propagation($W^TX+b$)으로는 정보를 전달할 수 없다. 그리고 length of capsule을 특정 entity가 존재할 확률이라고 했는데 확률은 [0, 1] 사이의 값을 가지지만 length of capsule은 1이상이 될 수도 있다.

• layer간의 차원이 다른 capsule의 forward propagation
• capsule의 길이를 [0, 1]사이 값으로 mapping

이 두가지문제를 해결하기위해 CapsNet에서는 새로운 학습 방식을 사용하는데 그것이 바로 capsule간의 Dynamic Routing이다.

Dynamic Routing

CapsNet에관한 유투브 영상 6개를 거의 3~4번씩은 봤는데 그 중에서 Dynamic Routing에대해 설명을 이해가 가장 잘된 동영상이 바로 Hands-on Machine Learning 저자 Aurélien Géron 의 유투브 동영상이다. 이 글을 읽고 이 동영상으로 확실하게 개념을 이해하면 완전하게 Dynamic Routing 개념을 이해할 수 있을 것이다. 물론 그 안의 수학적인 의미를 이해하기는 어렵겠지만 동작 개념을 이해하기엔 충분하다고 본다.

Squash function

Squash는 CapsNet에서 사용하는 activation function이다. capsule가 vector형태이니 당연히 ReLU나 Sigmoid를 사용하지못한다. 이 squash가 해주는 일은 바로 vector의 길이를 [0, 1]사이로 mapping해주는 역할을 한다. squash 함수의 식은 \(v_{j} = squash(s_{j}) = \frac{\left \| s_{j} \right \|}{1+\left \| s_{j} \right \|}\cdot \frac{s_{j}}{\left \| s_{j} \right \|}\)

오른쪽 부분은 unit vector를 만들어주는 식이고 왼쪽 부분은 $\left | s_{j} \right |$가 크면 1에 가깝게 작으면 0에 가깝게 크기를 조절해주는 scalar 값이다. 즉 어떤 vector가 들어와도 그 length를 확률처럼 [0, 1]사이 값으로 만들어준다.

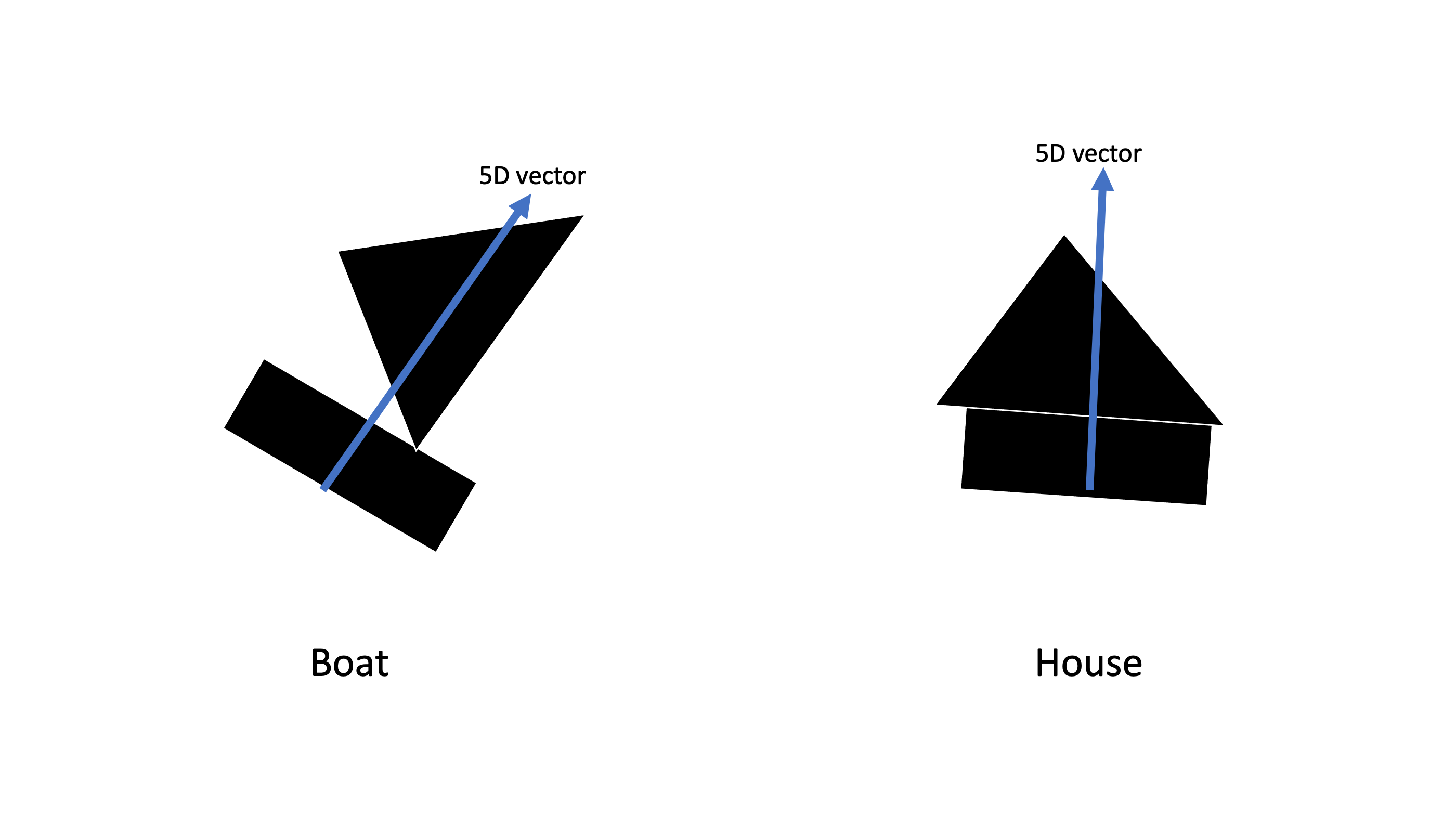
이렇게 Boat와 House entity가 있고 이 entity를 표현하기 위한 capsule의 instantiation parameter가 5개가 필요해서 각 entity의 vector가 5차원 벡터라고 하자. 그런데 이전 layer에 사각형과 삼각형의 capsule들이 있었다라고 생각해보자.

왼쪽의 저차원 capsule에 Affine Transformation을 해주는 matrix를 내적해서 각 캡슐이 다음 capsule로의 차원을 맞추어줄 수 있다. capsule vetor가 3D 에서 5D로 변환이 되어야하기 때문에 각 캡슐에 (5 by 3) matrix인 $W_i$를 내적해줘보자.

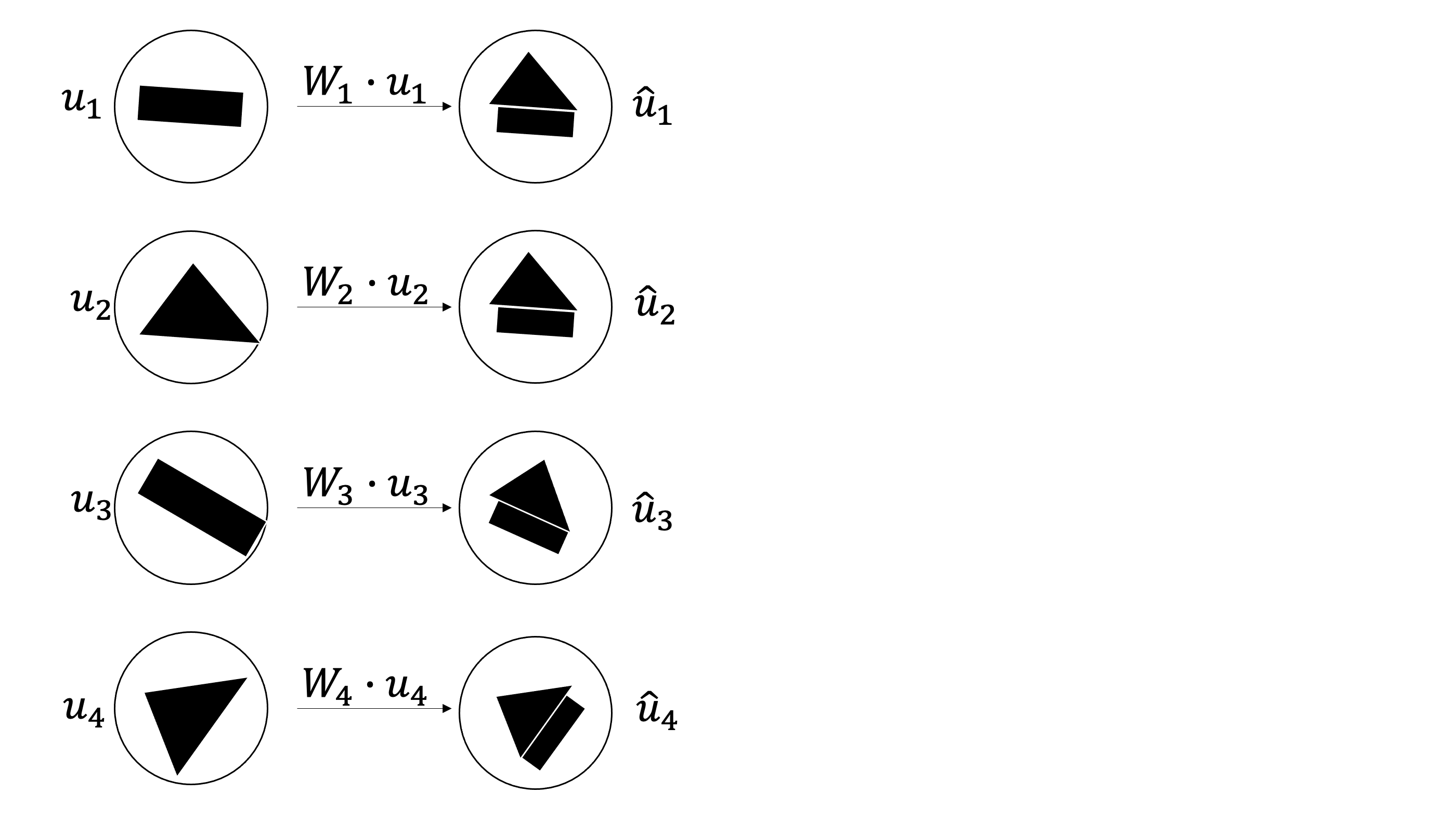
각 캡슐마다 차원을 늘려주는 Affine Transformation을 해줌으로서 다음 layer와의 계산을 원활하게 할 수 있게되었다. 위의 그림에서 “아니 사각형에다가 내적했는데 삼각형이 어디서 튀어나와서 집모양이되고 보트모양이되냐” 라고 의문을 가질 수 있다. 논문에서는 $\hat{u}$을 prediction vector라고 말한다. 왜냐하면 Affine Transformation의 역할은 단순이 차원을 늘려주는 역할 뿐만 아니라 현재 캡슐이 다음 캡슐이 어떤 모양일지 예측하게끔 학습을 시키기 때문이다. 즉 내적을 한 값은 현재 캡슐의 예측값이되고 위 이미지에서 내가 집으로 표현한것은 어디까지나 예시를 들기 위해서지 실제로 저런식으로 딱들어맞게 예측이 되지않는다(어차피 벡터는 이미지를 inverse rendering한 숫자들이기 때문에 어떤모양이든 될 수 있다).

위 이미지에서 1, 2 번째 예측은 서로 비슷한 예측을 했고 3, 4번의 예측들은 서로 전혀다르다. 이 때 서로 비슷한 예측을 한 capsule끼리 서로 agreement가 있다 라고 표현한다. 찌찌뽕을 생각하면 편하다.

각 capsule에서 뽑은 예측 벡터끼리 가중합을 해볼껀데 여기서 $b_i$와 $c_i$가 있는데, $c_i$는 $b_i$에 softmax를 취해준 값이다. $[c_1, c_2, c_3, c_4] = softmax([b_1, b_2, b_3, b_4])$ 이렇게 보면 된다. 여기서 헷갈릴 수 있는데 각 캡슐안의 도형들은 사실 벡터이기 때문에 껍데기만 도형이고 사실은 벡터라고 인지를 하고 보길 바란다.

\[s_j = c_{1}\hat{u}_{j|1}+c_{2}\hat{u}_{j|2}+c_{3}\hat{u}_{j|3}+c_{4}\hat{u}_{j|4}\] \[v_j = squash(s_j)\]

$v_j$는 이전 layer capsule들의 가중합인데 이전 layer에서 capsule끼리 agreement가 많았다면 $v_j$의 모양은 같은 agreement를 가졌던 capsule들의 모양과 비슷해질 것이다. 아래의 예시를 보자

agreement가 많은 capsule의 예시

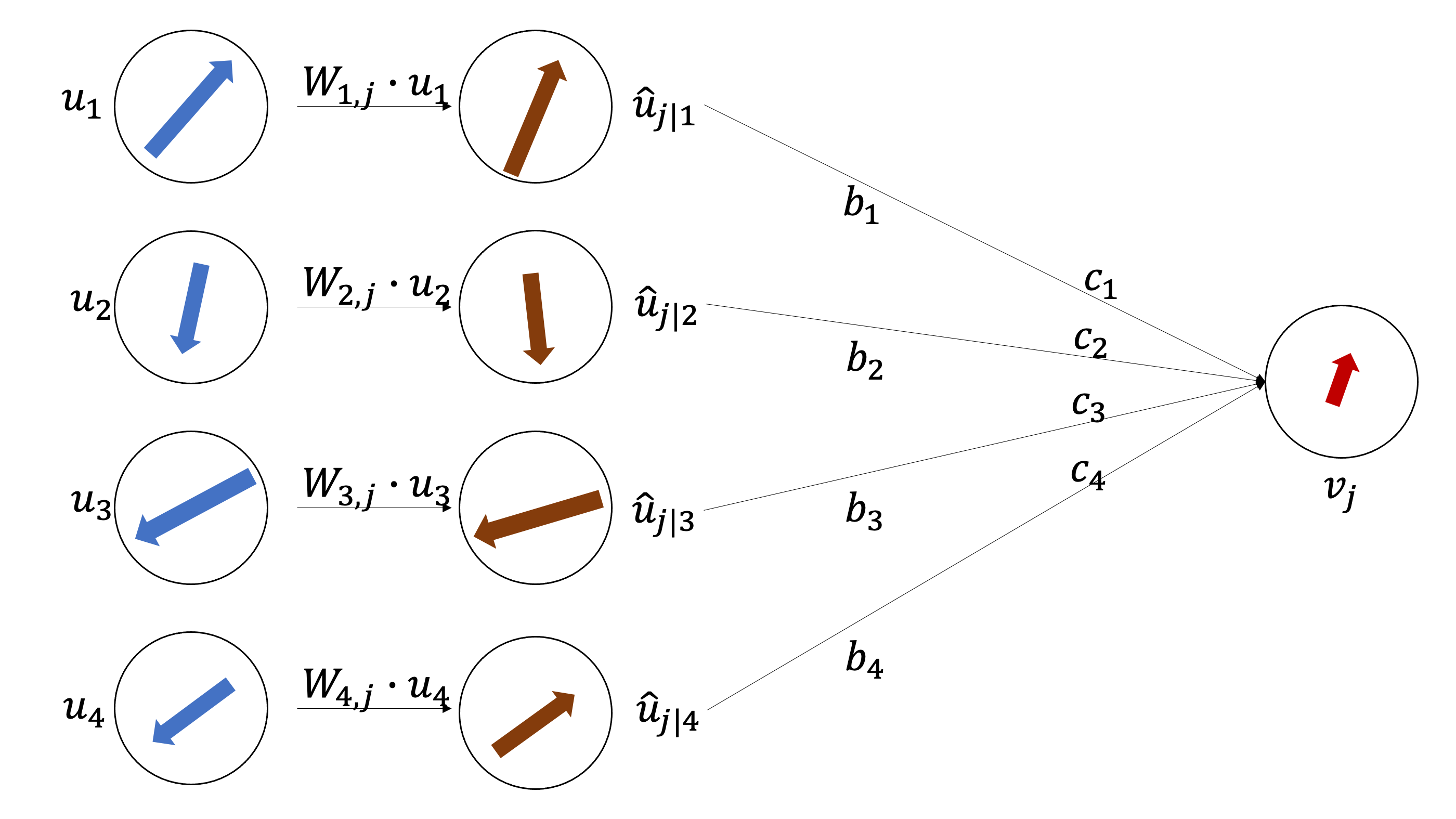
agreement가 적은 capsule의 예시

우선 $v_j$의 길이가 너무 0에 가깝게 너무 작으면 아예 $v_j$ capsule은 activate되지 않게된다. 그리고 $v_j$는 agreement가 같은 벡터들에 dependent하게 형성이 된다. 논문에 나온 $b_i$를 업데이트하는 식을 보자. \(b_{ij}\leftarrow b_{ij} + \hat{u}_{j|i} \cdot v_{j}\\\)

$b_{ij}$는 capsule들의 가중치인데 내적을 통해 값을 증가시켜주고 있다. 여기서 \(\hat{u}_{j|i} \cdot v_{j}\) 의미를 살펴보자
\(cos\theta = \frac{\vec{a}}{\left \| a \right \|}\cdot \frac{\vec{b}}{\left \| b \right \|}\\ k\ cos\theta = \vec{a} \cdot \vec{b}\\\)

두 벡터의 내적은 각도가 비슷할수록 커지게된다. 그렇다면 $b_{ij}$를 업데이트하는 과정에서 이전 layer 캡슐의 예측 벡터와 다음 layer의 캡슐의 내적합으로 update가 되는데 비슷한 캡슐의 가중치는 커지게되고 모양이 다른 벡터의 가중치는 조금씩 커지게되는데 여기서 $softmax$를 먹여버리면 작은놈은 계속 작아지고 큰놈은 계속 커지게된다. 마치 SequenceToSequence 의 attention 메커니즘과 비슷한 방식이 되는 것이다.

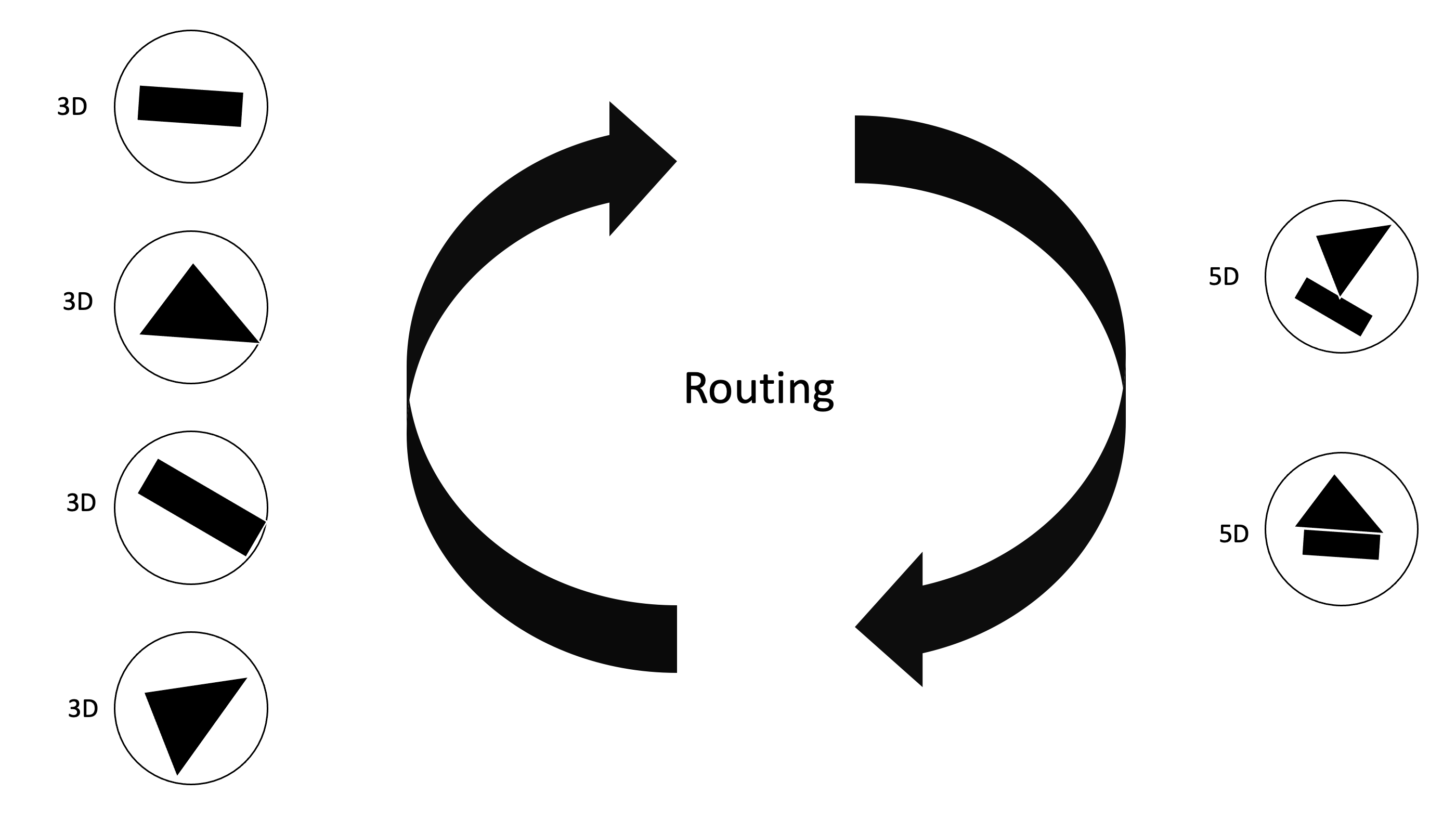
Routing Algorithm은 기존의 Network들처럼 feed forward하게 값을 전달하는 것이아닌 각 레이어마다 내부에서 반복적으로 Routing이 일어나게된다. 각 Layer사이에서 Routing이 반복적으로 일어나게되면

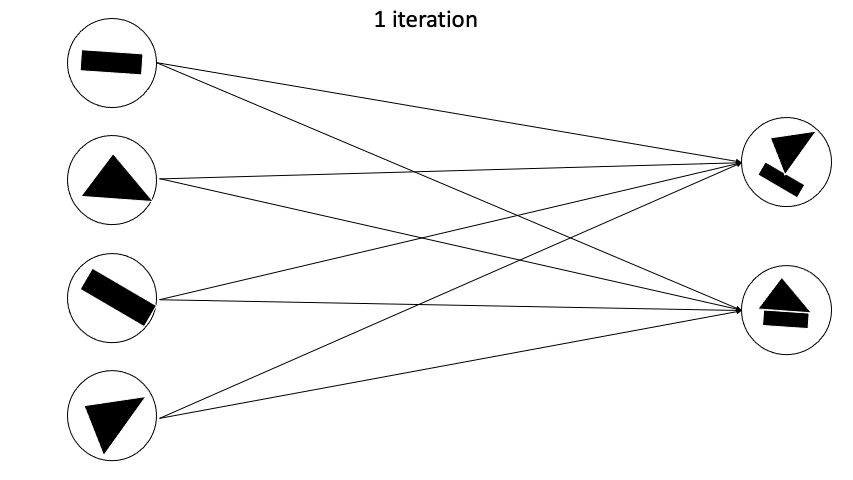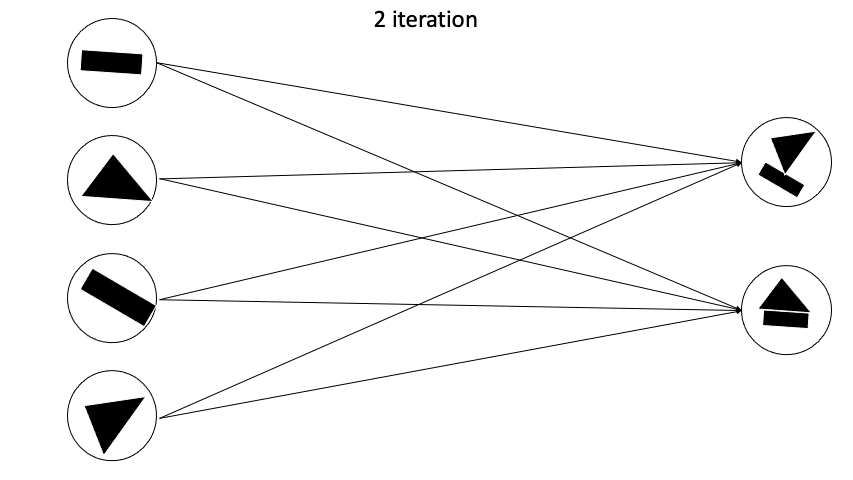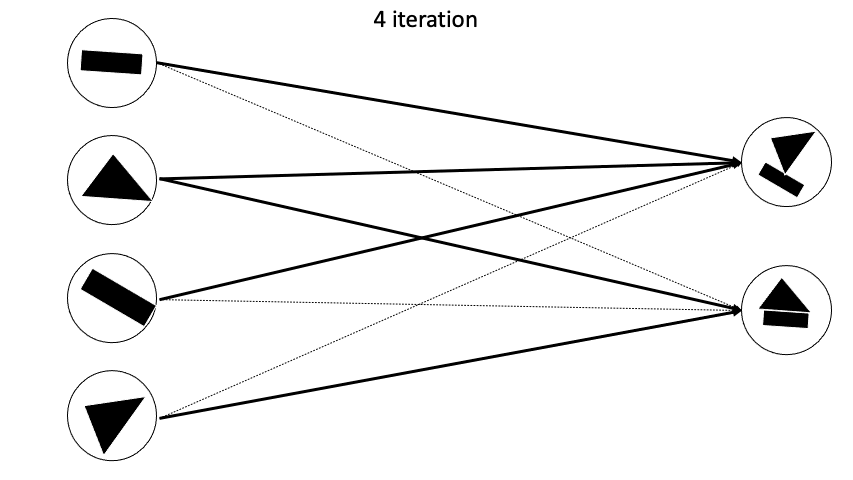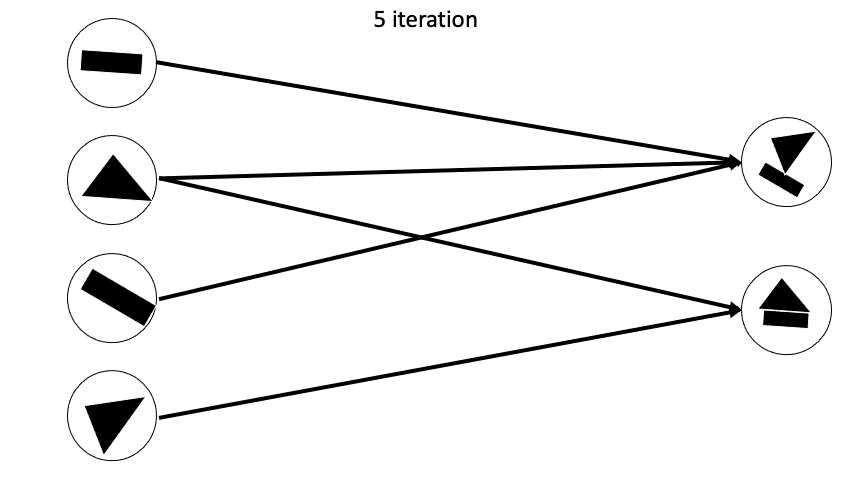
이렇게 Fully Connected 형태가 아니게되고 agreement한 capsule끼리 새로운 다음 layer capsule을 만들어나가게 된다.

이게 논문에 나와있는 수도코드인데 이해할 수 있을꺼라 생각한다. 여기서 r은 routing을 몇번할것인지에 대한 hyper parameter이다.

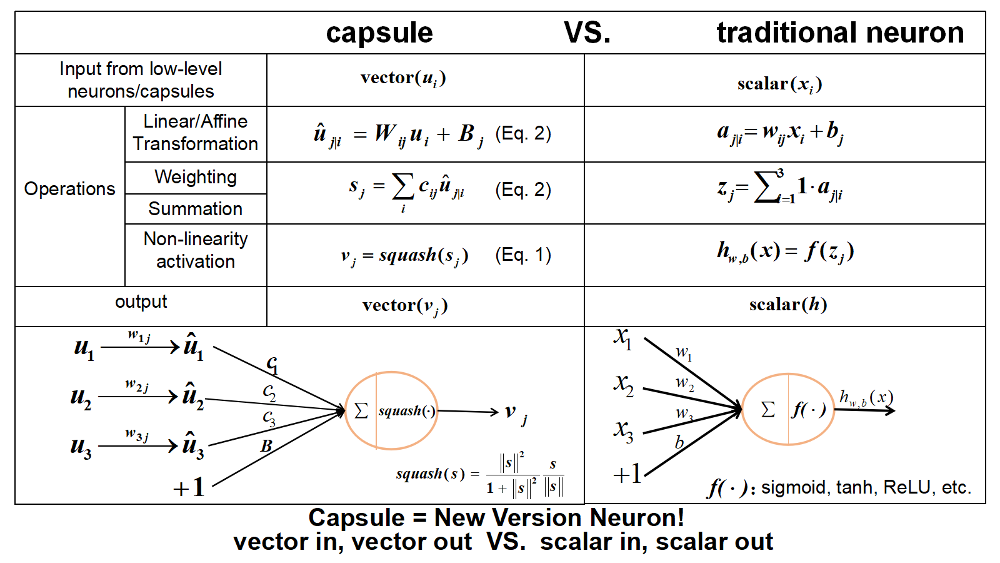
이미지에 잘못 표기되어있는데 CapsNet에는 bias가 업다

Loss Function

CapsNet의 Loss Function은 Margin Loss + Reconstruct Loss를 이용해 파라미터를 update한다. 파라미터는 2가지다.

• 제일처음 Conv feature maps를 만들 때 사용한 filter들
• Predict Matrix(Affine Transformation) $W$

Margin Loss(Supervised Loss Function)

Margin Loss의 공식은 다음과 같다

\[L_{k} = T_{k}\ max(0, m^{+}-\left \| v_{k} \right \|)^2\ +\ \lambda (1-T_{k})max(0, \left \| v_{k} \right \|)-m^{-})^2\]

• $m^+ = 0.9$
• $m^- = 0.1$
• $\lambda = 0.5$
• $v_k$ : 마지막 layer의 k번째 capsule

의미 : 정답 label의 예측 벡터의 길이(확률)는 최대 0.9가 되도록 만들고, 정답레이블이 아닌 나머지 label의 예측 벡터의 길이는 최소 0.1이 되도록 만들겠다.

CapsNet의 마지막 레이어는 label 개수만큼의 encoding된 capsule들이 존재한다. MNIST를 예로 들어보자

그런데 의문인 것은 분명 논문에는 The total loss is simply the sum of the losses of all digit capsules.이라고 나와있어서 저렇게 이해했는데 식에는 막상 오답레이블에대한 $\sum$ 이 없다. 잘못 이해한건가 아니면 너무 당연해서 뺀건가.. 그건 잘 모르겠다

Reconstruction Loss(Unsupervised Loss Function)

이부분이 제일 흥미로우면서도 재밌는 부분이었다. 위에서 entitiy를 벡터로 inverse rendering을 하는것이 CapsNet이라고 했는데, 그렇다면 capsule을가지고 entity를 rendering할 수도 있다는 말이다. decoding 하는 과정을 reconstruction이라고 하는데

이렇게 reconstruct Image와 Input Image와의 픽셀값 차이($L_2$)거리도 Loss함수에 넣어준다.

• $\alpha = 0.0005$
• $X$ : input image
• $X_{r}$ : reconstruct image

Capsule Network Architecture

논문의 사진을 그대로 가져왔다. 논문에서는 MNIST 데이터셋을 기준으로 설명을 했고 저렇게 구조를 만들었는데

• Input 이미지로부터 Conv2d(1, 256, kernel_size=9, padding=0, stride = 1) 필터로 feature maps를 만들어준다.
• feature maps로 부터 Conv2d(1, 256, kernel_size=9, padding=0, stride = 2) 필터로 feature maps를 만들어준다.
• 2번째 feature maps를 reshape 해준다.

코드를 보면 이런식으로 reshape을 해주어서 $W$와 내적하고 Routing을 한다. 이렇게 CapsNet 구조에대한 설명을 끝냈고 CapsNet의 성능 및 강점, 단점 등등 실험결과를 다음 포스트에서 마저 하도록 하겠다.