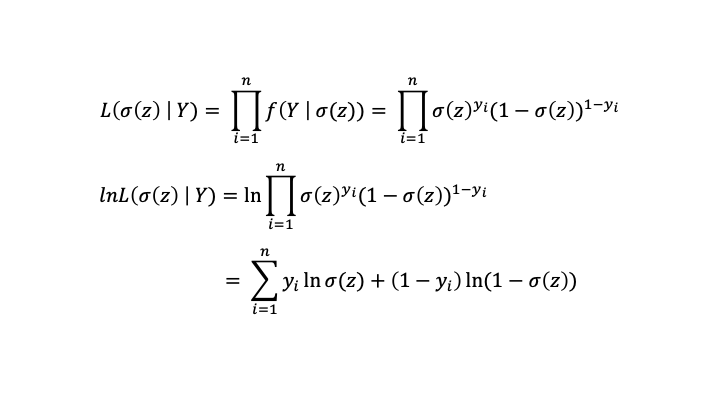Logistic function(sigmoid)
logistic function은 실수 전체집합 $x$를 [0, 1] 사이 값으로 출력해주는 함수다.
\[y = \frac{1}{1+e^{-x}}\]
Odds
흔히 도박 배당률에서 볼 수 있는 수학적인 비율이다.
어떤 사건 $A$가 발생할 확률 = $P(A)$
어떤 사건 $A$가 발생하지 않을 확률 = $1-P(A)$
$Odds = \frac{P(A)}{1-P(A)}$
$(Odds \ge 0)$ 인 범위를 가진다
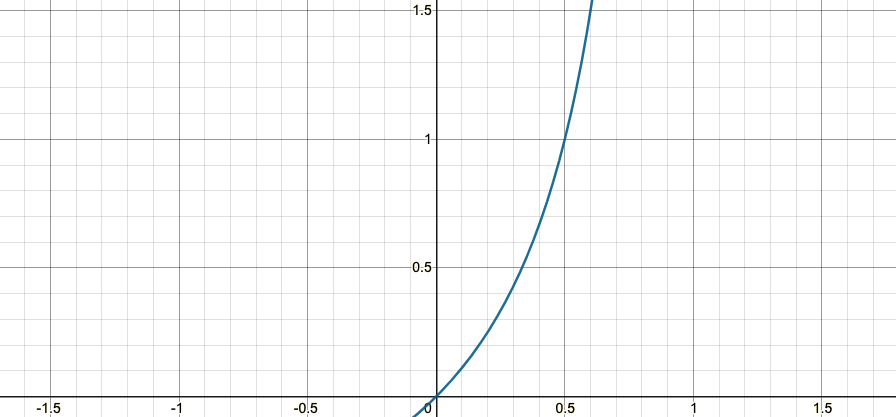
Logistic Regression 판별함수
Linear Regression 의 식
$y = W^TX + b$
Linear Regression은 범주형 $target$ 에적합하지 않다. 범주형 $target$의 1 과 0은 숫자의 크기가 아닌 yes or no의 성질을 가지 때문에 \(target, y\)를 회귀에 적용시키려면 성질을 변화시켜주어야한다. 그래서 $y \rightarrow Odd(y)$로 변화시키면
\[\frac{P(y = 1 | X)}{1-P(y = 1 | X)} = W^TX + b\]
하지만 문제는 좌변의 범위는 [0, inf] 인데, 우변의 범위는 [-inf, inf] 라 범위가 맞지 않는다. 그래서 좌변에 $log$를 씌워 방정식을 맞춰주고 정리하면
\[z = W^TX + b\] \[P(y = 1 | X) = \sigma(z) = \frac{1}{1 + e^{-z}}\]
$y$가 발생할 확률을 위에서 봤던 Logistic Function으로 매칭시킬 수 있게된다. 그리고 바로 이 Logistic Function값이 0.5를 기준으로 넘나 안넘나를 가지고 $y$가 $1$인지, $0$인지 판별한다.
$1\, \, if \, \sigma(z) > 0.5 \, else \, 0$
$1\, \, if \, z > 0 \, else \, 0$
LR Parameter Update
Linear Regression의 손실함수는 $MSE$를 쓰지만, Logistic Regression의 손실함수는 로그 손실함수라는 독자적인 손실함수를 이용해 파라미터($W, b$)를 갱신한다.
Likelihood
likelihood개념을 이해하기 가장 좋은 블로그
성공(1), 실패(0)에 관한 확률분포인 베르누이 확률밀도함수를 보자.
$f(X, p) = p^{x} (1-p)^{1-x}$
$X = 1 \, or \, 0$
베르누이 확률밀도함수의 확률변수는 $X$, 그리고 파라미터는 성공할 확률인 $p$가 된다. 이것을 LR 파라미터로 바꿔보자.
$f(y, \sigma(z)) = \sigma(z)^{y} (1-\sigma(z))^{1-y}$
$y = 1 \, or \, 0$
$\sigma(z)$는 파라미터고, 이미 주어진 관찰값(데이터 표본)들로 $\sigma(z)$를 추정해야하는데
- 점추정
- 구간추정
- moment 추정
- MLE
MLE를 쓴다. 왜인지는 나도 자세히 모른다.
로그 likelihood
MLE
Maximum likelihood를 구하기 위해 $W, b$로 미분을 해야한다.
update
\(lnL(\sigma(z) \mid Y)\)의 값이 최대가 되는 방향으로 파라미터 $W, b$를 업데이트 해야하기 때문에
$W_{k+1} = W_{k} + \eta \sum (y_{i}-\sigma(z))x_{i}$
$b_{k+1} = b_{k} + \eta \sum (y_{i}-\sigma(z))$
Logistic 구현
import matplotlib.pyplot as plt
import numpy as np
import random
class LR :
def __init__(self) :
self.W = None
self.b = None
self.loss = []
def forward(self, x):
z = np.sum(x * self.W) + self.b
return z
def back(self, x, err):
w_grad = err * x
b_grad = err
return w_grad, b_grad
def sigmoid(self, z) :
return 1/(1 + np.exp(-z))
def fit(self, X, Y, epochs=1000, lr = 0.01):
self.W = np.random.normal(size = X.shape[1])
self.b = random.random()
for _ in range(epochs):
for x, y in zip(X, Y):
z = self.forward(x)
err = y - self.sigmoid(z)
w_grad, b_grad = self.back(x, err)
self.W += lr * w_grad
self.b += lr * b_grad
self.loss.append(err)
def predict(self, X):
z = [self.forward(x) for x in X]
return [1 if self.sigmoid(z_) >= 0.5 else 0 for z_ in z]
def lossgraph(self) :
x = range(len(self.loss))
plt.plot(x, self.loss, 'ro')