최적 행렬곱셈 업그레이드 문제. 하지만 2가지 풀이가 존재한다.
import re
def solution(arr):
num = re.findall('\d+', (k := ''.join(arr)))
sign = re.findall('\D', k )
n = len(num)
dp_max = [[-1e9]*n for _ in range(n)]
dp_min = [[1e9]*n for _ in range(n)]
for i in range(n) :
dp_max[i][i] = int(num[i])
dp_min[i][i] = int(num[i])
for gap in range(1, n) :
for i in range(n-gap) :
for k in range(i, (j := i+gap)) :
if sign[k] == '+' :
dp_max[i][j] = max(dp_max[i][j], dp_max[i][k] + dp_max[k+1][j])
dp_min[i][j] = min(dp_min[i][j], dp_min[i][k] + dp_min[k+1][j])
else :
dp_max[i][j] = max(dp_max[i][j], dp_max[i][k] - dp_min[k+1][j])
dp_min[i][j] = min(dp_min[i][j], dp_min[i][k] - dp_max[k+1][j])
return dp_max[0][-1]
\(O(n^3)\) 알고리즘
dp_max[i][j]:i번째 숫자부터j번째 숫자까지 계산했을 때 최대값
dp_min[i][j]:i번째 숫자부터j번째 숫자까지 계산했을 때 최소값숫자 사이 부호가
+일경우
dp_max[i][j] = max(dp_max[i][j], dp_max[i][k] + dp_max[k+1][j]) # 큰수 + 큰수 dp_min[i][j] = min(dp_min[i][j], dp_min[i][k] + dp_min[k+1][j]) # 작은수 + 작은수숫자 사이 부호가
-일경우
dp_max[i][j] = max(dp_max[i][j], dp_max[i][k] - dp_min[k+1][j]) # 큰수 - 작은수 dp_min[i][j] = min(dp_min[i][j], dp_min[i][k] - dp_max[k+1][j]) # 작은수 - 큰수
\(O(n)\) 알고리즘
def solution(arr):
y = prev_max = prev_sum = 0
for sign, x in zip(arr[-2::-2], arr[-1::-2]):
x = int(x)
if sign == '+':
y += x
else:
prev_max = -x + max(y + prev_max, -y + prev_sum)
prev_sum += y + x
y = 0
return int(arr[0]) + y + prev_max
해설
+ 와 - 로만 이루어진 임의의 다항식이 있다.
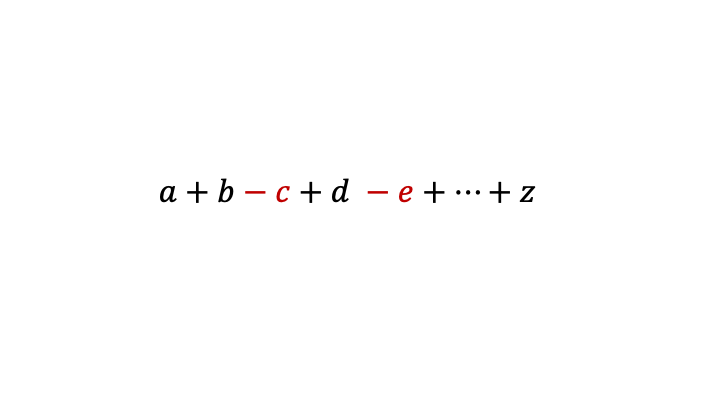
목표는 뺄셈은 결합법칙이 성립하지않는 특성을 이용해 다항식의 최대값을 구하는 것이다.
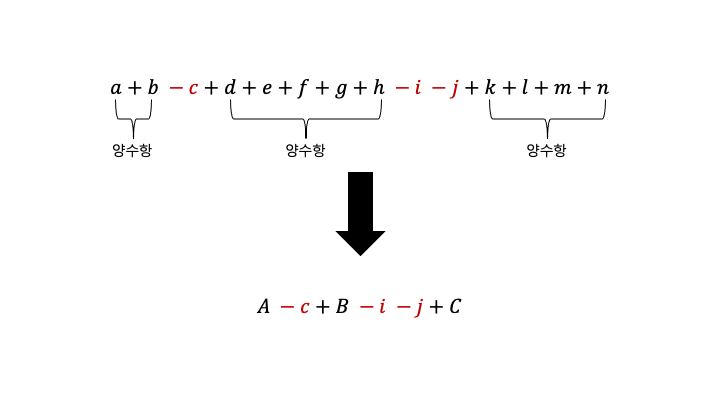
양수항은 결합법칙에 아무런 영향도 주지 않기 때문에 이렇게 양수항을 합쳐주고 계산할 수 있다.
일반화

x: 부호가 음수인 정수
y: 부호가 양수인 정수
a: 제일 앞의 수(양수든 정수든 상관없음)
여기서 결합법칙 트릭을 이용해서 이 식을 이렇게 바꿀 수 있다.

max_xi : (오른쪽에서 왼쪽으로 계산했을 때)xi항까지 계산한 최대값 sum_xi : sum(xi + yi + ... x0 + y0)
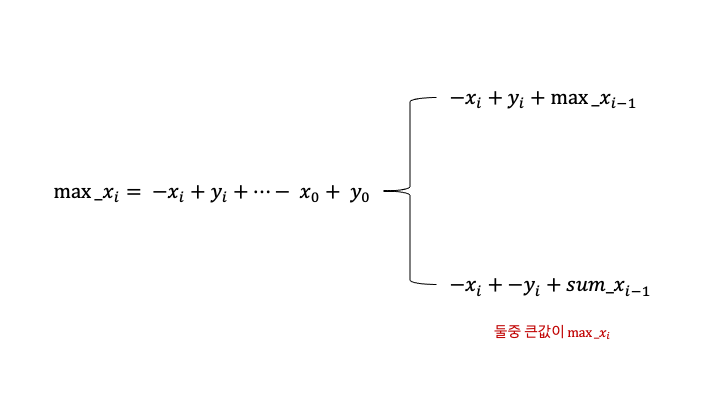
\[\begin{align} &max\_x_{i}\,=\,-x_{i}\,+\,max(y_i\,+\,max\_x_{i-1},\,-y_{i}\,+ sum\_x_{i-1})\\ &sum\_x_{i}\,=\,x_{i}\,+\,y_{i}\,+\,sum\_x_{i-1}\\ \end{align}\]
코딩을 해야하기 때문에 변수명을 쪼금 바꿨지만 알고리즘은 동일하다
def solution(arr):
y = prev_max = prev_sum = 0
for sign, x in zip(arr[-2::-2], arr[-1::-2]):
x = int(x)
if sign == '+': # 양수항 합치기
y += x
else: # 음수 x 를 만났을 때
prev_max = -x + max(y + prev_max, -y + prev_sum)
prev_sum += y + x
y = 0
return int(arr[0]) + y + prev_max