from collections import defaultdict, deque
from copy import deepcopy
def level(node, levels) :
levels[node] = -1
que = deepcopy(graph[node])
level = 0
while que :
for _ in range(len(que)) :
child = que.popleft()
if not levels[child] :
levels[child] = level + 1
que.extend(deepcopy(graph[child]))
level += 1
return levels
def solution(n, edges):
global graph
graph = defaultdict(deque)
for v1, v2 in edges:
graph[v1-1].append(v2-1)
graph[v2-1].append(v1-1)
v1 = level(0, [0]*n)
v2 = level(v1.index(max(v1)), [0]*n)
if v2.count((max_ := max(v2))) >= 2 :
return max_
else :
v3 = level(v2.index(max_), [0]*n)
return max_ if v3.count((max_ := max(v3))) >= 2 else max_ - 1
트리의 지름
출제의도를 알았다면 금방 풀 수 있는 문제였지만 그걸 알아차리지 못했다. 문제에서는 세점을 골랐을 때 최대의 중간값을 구해라라는 문제처럼 보이지만 진정한 뜻은
트리의 지름을 구성하는 노드가 유일한가 아닌가?
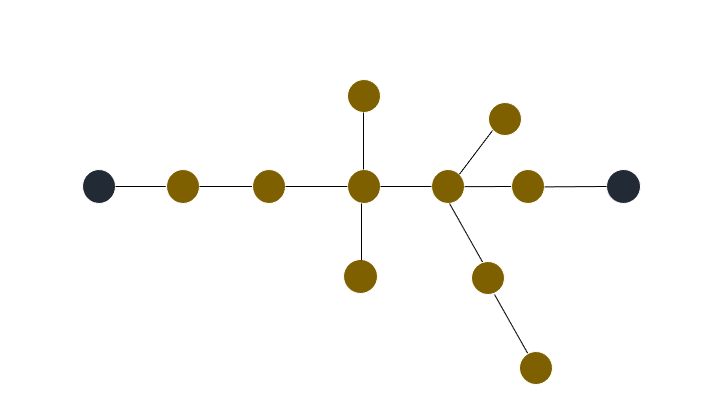
트리를 펼쳤을 때, 두 노드의 거리가 가장 긴 거리를 트리의 지름이라고 한다.
중간값(중앙값, median)
[1, 99, 100]
median = 99
중간값은 평균과 다른 정의를 가진다. 말 그대로 원소중에서 중간순위에 있는 원소를 말한다.
그렇다면 트리의 지름과 문제에서 묻는 최대 중간값이 무슨관계가 있을까?
트리의 지름과 최대 중간값
트리의 3개의 노드 v1, v2, v3 가 있다.
각 노드사이 거리를 구하는 함수를
d트리의 지름을 구성하는 노드
v1,v3, 트리의 지름 =D
d(v1, v2), d(v2, v3), d(v3, v1) = d(v1, v2), d(v2, v3), D
최대의 중간값은 v2에 달렸는데, v2가 될 수 있는 경우는 단 2가지가 있다.
(v1, v2)or(v2, v3)이 트리의 지름을 이루는 노드
d(v1, v2), d(v2, v3), d(v3, v1) = D, d(v2, v3), D
v2가v1orv3와 거리차이가1만큼 나는 노드
d(v1, v2), d(v2, v3), d(v3, v1) = D-1, d(v2, v3), D
즉, 최대 중간값은 트리의 지름을 구성하는 노드가 한쌍인지, 아니면 여러쌍이 있는지에대한 문제입니다.
트리의 지름을 구성하는 노드가 한쌍인 경우 =
D-1트리의 지름을 구성하는 노드가 여러쌍인 경우 =
D
알고리즘
- 임의의 한점에서 가장 먼 점
v1선택(v1가 여러개라도 상관없음)v1에서 가장 먼 점v2구함v2가 여러개라면 트리의 지름을 이루는 노드가 여러쌍, 답 :Dv2가 하나라면 다시v2에서 가장 먼 노드v3를 구함
v3가 여러개라면 트리의 지름을 이루는 노드가 여러쌍, 답 :Dv3가 하나라면 트리의 지름을 이루는 노드가 한쌍, 답 :D-1
여기서 아니 왜 한점에서 가장먼 노드찾아내는게 트리의 지름을 구하는거임? 이라는 의문을 가지는게 당연하다. 트리의 지름을 구하는데에는 사실 가장 먼노드를 2번만 구하면 된다. 2번만 하면 트리의 지름이 나오는 이유
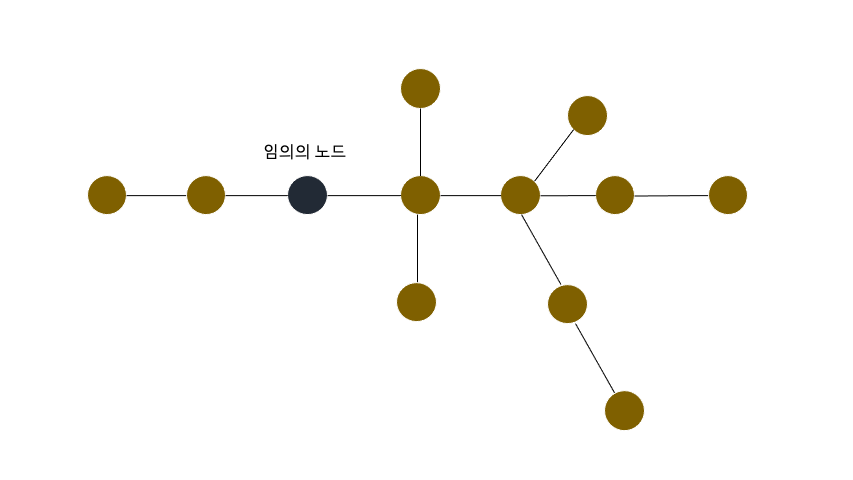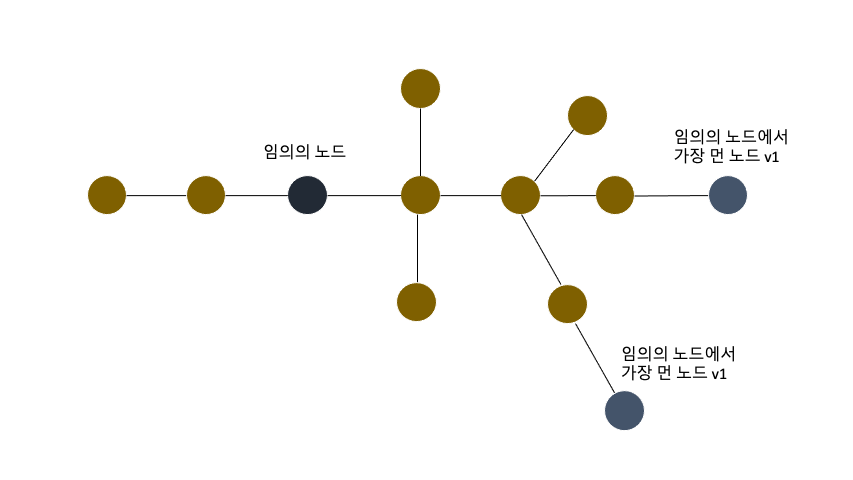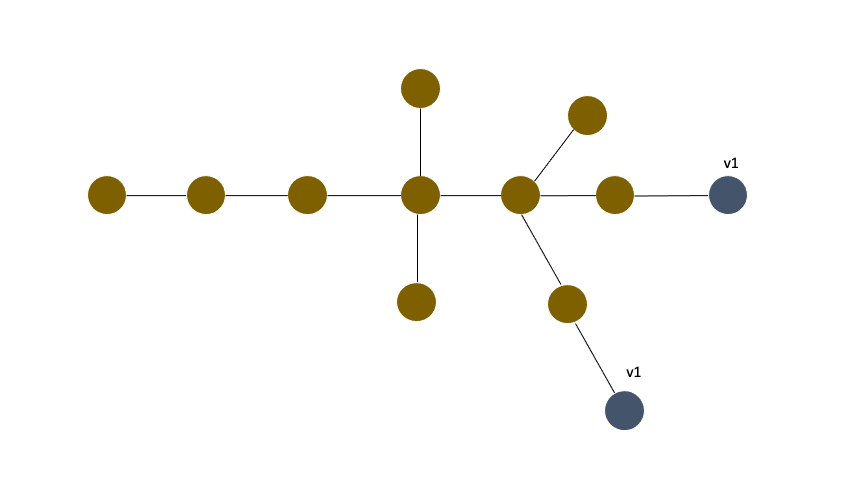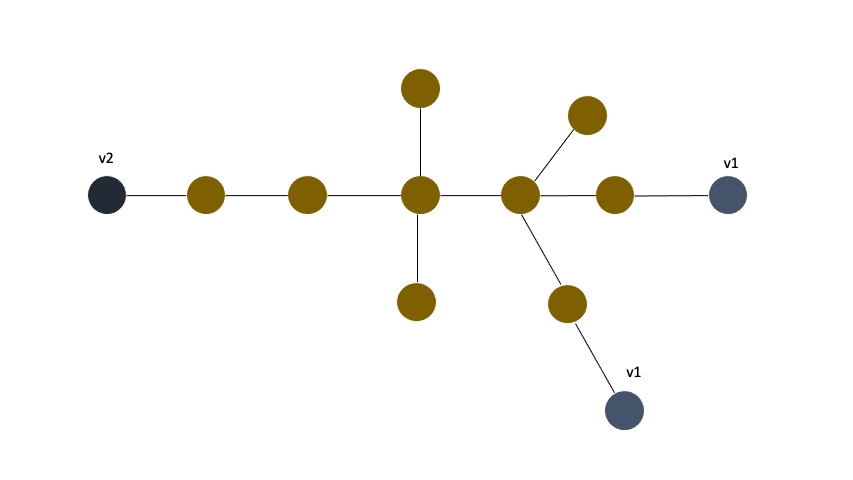
이렇게 2번만 하면 지름을 구할 수 있지만, 지름을 구성하는 노드가 몇쌍인지를 모르는 경우가 생긴다. 그래서 총 3번 노드에서 가장먼노드를 찾는거다.
from collections import defaultdict, deque
from copy import deepcopy
def d_list(node, d) : # BFS로 node기준 다른 노드들의 거리list를 구하는 함수
d[node] = -1
que = deepcopy(graph[node])
dist = 0
while que :
for _ in range(len(que)) :
child = que.popleft()
if not d[child] :
d[child] = dist + 1
que.extend(deepcopy(graph[child]))
dist += 1
return d
def solution(n, edges):
global graph
graph = defaultdict(deque)
for v1, v2 in edges:
graph[v1-1].append(v2-1)
graph[v2-1].append(v1-1)
v1 = d_list(0, [0]*n) # 임으의 node 0 에서 거리 리스트 v1 구함
v2 = d_list(v1.index(max(v1)), [0]*n) # v1에서 거리 리스트 v2
if v2.count((D := max(v2))) >= 2 : # v2 최대값이 여러개면 D
return D
else : # v3 찾고, 최대값 구하기
v3 = d_list(v2.index(D), [0]*n)
return D if v3.count((D := max(v3))) >= 2 else D - 1