def solution(matrix_sizes):
n = len(matrix_sizes)
d = matrix_sizes[0] + [x[1] for x in matrix_sizes[1:]]
dp = [[0]*n for _ in range(n)]
for gap in range(1, n) :
for i in range(n-gap) :
for k in range(i, (j := i+gap)) :
l = dp[i][k] + dp[k+1][j] + d[i]*d[k+1]*d[j+1]
dp[i][j] = min(dp[i][j], l) if dp[i][j] else l
return dp[0][-1]
DP의 뜻
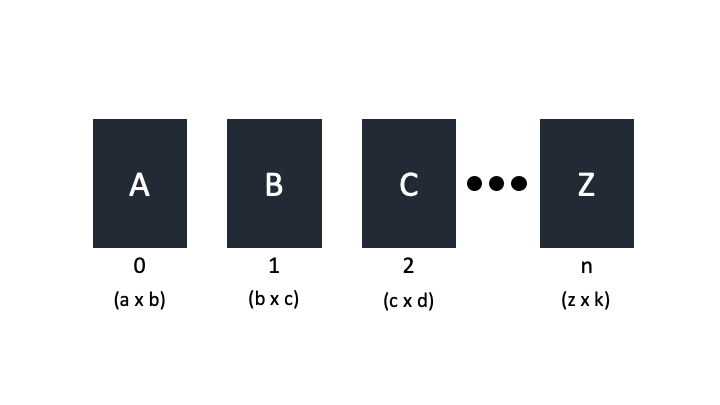
DP[i][j]:i행혈부터j행혈까지의 곱셉 횟수
- ex)
DP[0][2] = a*b*c + a*c*d
최소 곱셈횟수
행렬 A, B, C 가 있다.
행렬의 곱셈 순서를 달리하는 것만으로 곱셈 연산의 횟수가 달라진다.
그렇다면 n개의 행렬에서 최소 곱셈 횟수를 구하려면
\(\begin{align}
(((AB)C)D)\cdots N\\
((A(BC))D)\cdots N\\
(A(B(CD)))\cdots N\\
A(B(C(D(\cdots N))))\\
\end{align}\)
이렇게 모든 종류를 다 파악해주어야한다.
이를 수식으로 표현하면
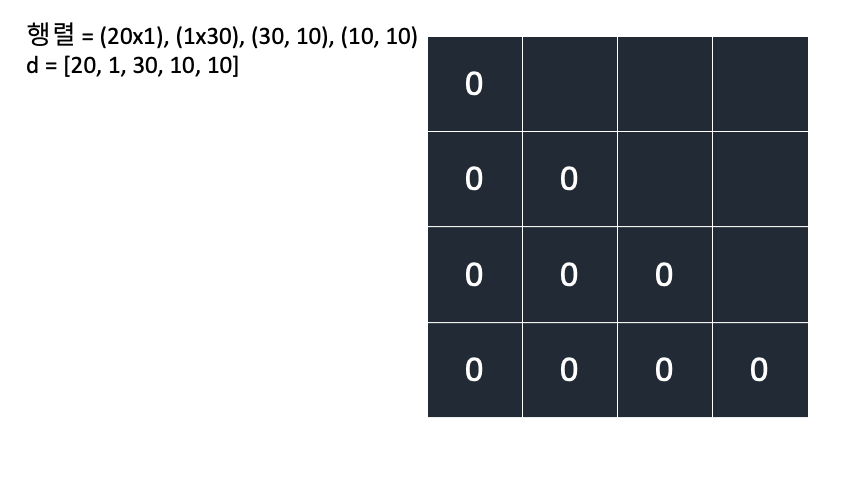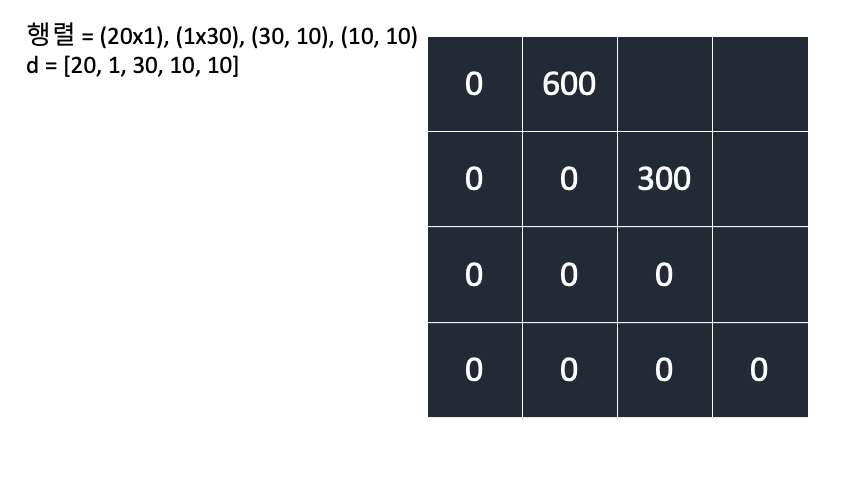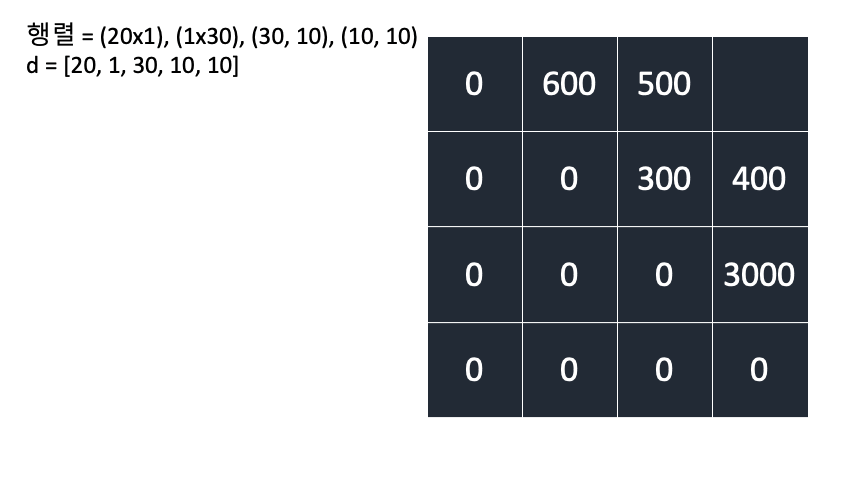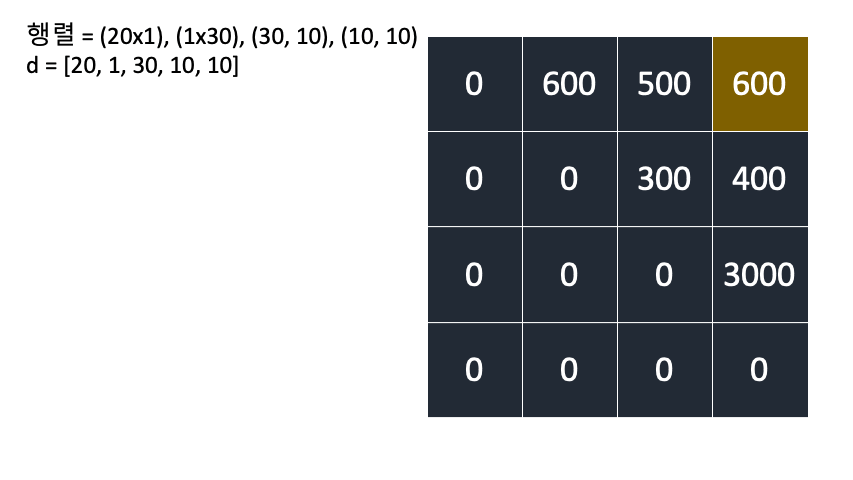
A(2x3),B(3x2),C(2x4)
d = [2, 3, 2, 4]
\[\begin{align} DP[i][j] = min(DP[i][k] + DP[k+1][j] + d[i]d[k+1]d[j+1])\\ (i \leq k < j,\,i < j)\\ \end{align}\]
(
DP[i][j]:i행렬에서j행렬까지 곱셈 횟수)
def solution(matrix_sizes):
n = len(matrix_sizes)
d = matrix_sizes[0] + [x[1] for x in matrix_sizes[1:]]
dp = [[0]*n for _ in range(n)]
for gap in range(1, n) :
for i in range(n-gap) :
for k in range(i, (j := i+gap)) :
l = dp[i][k] + dp[k+1][j] + d[i]*d[k+1]*d[j+1]
dp[i][j] = min(dp[i][j], l) if dp[i][j] else l
return dp[0][-1]