def solution(n):
if n%2 != 0 : return 0
n_2 = 3
n_1 = 11
for i in range(3, n//2+1) :
n_1, n_2 = (4*n_1 - n_2) % 1000000007, n_1
return n_1
탈인간 코드. 어떻게 이런 패턴을 발견한건지 경이로워서 가져와봄. 이거패턴 무슨 방식인지 좀 알려주셈 난 도저히 모르겠음
def solution(n):
pa, pb, pc, a, b, c = 1, 0, 0, 0, 0, 2
for _ in range(1, n):
pa, pb, pc, a, b, c = a, b, c, (c + pa) % 1000000007, c, (b + a * 2) % 1000000007
return a
짝수일때만 가능
해보면 알겠지만 짝수일 때는 빈칸이 1칸남아서 불가능하다. 따라서 모든 짝수 n은 n//2로 계산하겠다.
고유모양
n >= 2 부터는 이전 n들의 조합으로 만들 수 없는 고유모양이 2개씩 존재한다.
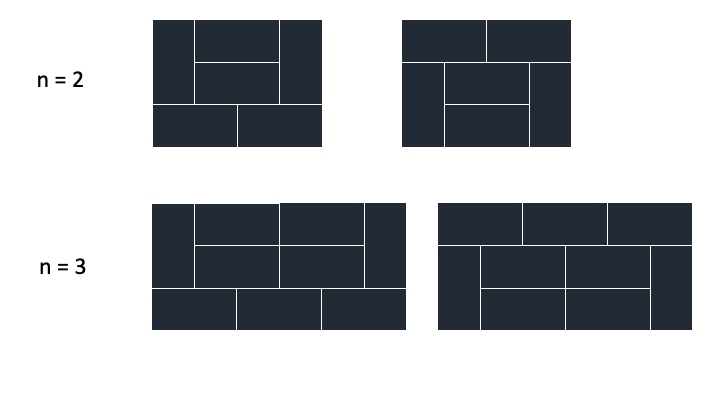
그 이유는 모든 타일은 이전 타일들의 조각으로 합칠 수 있다.

하지만 조각 사이사이틈이 다 막힌 모양은 단 2가지만 존재한다.
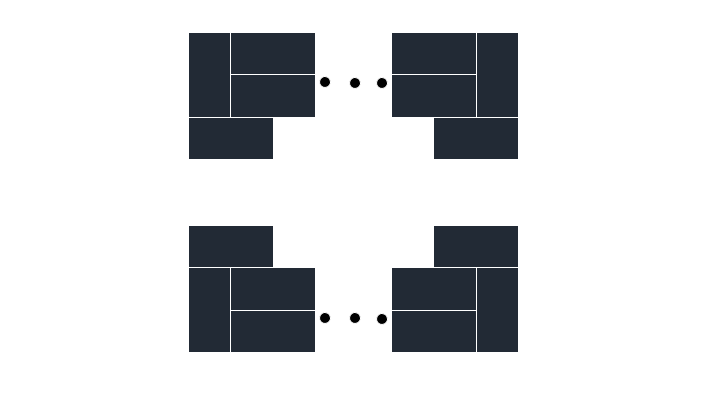
패턴
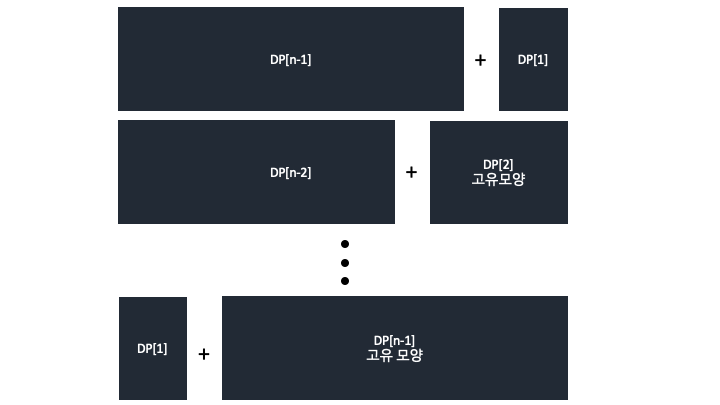
점화식을 이렇게 세울 수 있다. \(DP[N] = DP[N - 1] * DP[1] + DP[N - 2] * 2 + DP[N - 3] * 2 + \cdots + DP[1] * 2 + 2\\ DP[N] = 2(DP[N-2] + DP[N-3] + \cdots + DP[1]) + 3DP[N-1] + 2\\\)
\[DP[N] = 2(DP[N-2] + DP[N-3] + \cdots + DP[1]) + 3DP[N-1] + 2\\ DP[N-1] = 2(DP[N-3] + DP[N-4] + \cdots + DP[1]) + 3DP[N-2] + 2\\ DP[N]-DP[N-1] = 2DP[N-2] + 3DP[N-1] - 3DP[N-2]\\ DP[N] = 4DP[N-1] - DP[N-2]\\ (DP[1] = 3, DP[2] = 11)\\\]그리고 점화식이므로 일반식으로 만들 수 있다.
수식 왼쪽정렬시키는 법을 모르겠음 ㅅㅂ
def solution(n):
if n%2 != 0 : return 0
n_2 = 3
n_1 = 11
for i in range(3, n//2+1) :
n_1, n_2 = (4*n_1 - n_2) % 1000000007, n_1
return n_1