def queens(n, board, h) :
ans = 0
if h == n :
return 1
for w in range(1, n+1) :
board[h + 1] = w
if promising(board, h+1) :
ans += queens(n, board, h+1)
return ans
def promising(board, h) :
for h_ in range(1, h) :
if (w_ := board[h_]) == (w := board[h]) or h - h_ == abs(w_ - w) :
return False
return True
solution = lambda n : queens(n, [0]*(n+1), 0)
Promising?
한 행에 퀸을 하나씩 둔다.
퀸을 둘 때 현재의 위치가 유망하다면 다음행으로 진행하고, 유망하지 않다면 진행하지 않는다.
그렇다면 현재 두는 퀸이 유망한지 안한지는 어떻게 판별할까. 임의의 한 행의 퀸의 위치를 (h_, w_), 현재 내가둘 퀸의 위치를 (h, w)로 보겠다.
두 퀸이 같은 열에 있으면 유망하지 않다.
if w == w_ : non_promising두 퀸이 같은 대각선상에 있으면 유망하지 않다.
if h_ - h == abs(w_ - w) : non_promising
- 대각 검사는 말과 말의 행간의 거리와 열간의 거리가 같은지 검사
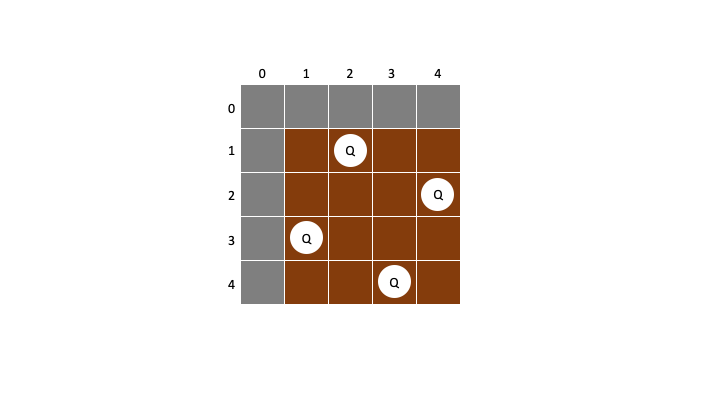
이 promising검사를 현재둘 퀸 이전 행의 퀸들과 검사하며 모든 과정을 마쳤을 때 이러한 배치가 나올 것이다.
그런데 굳이 2차원 배열을 쓸필요가 있을까? 각 Queen에 자신의 열에대한 정보를 담아준다면 promising검사도 가능하고 코드도 간결해 질것이다.
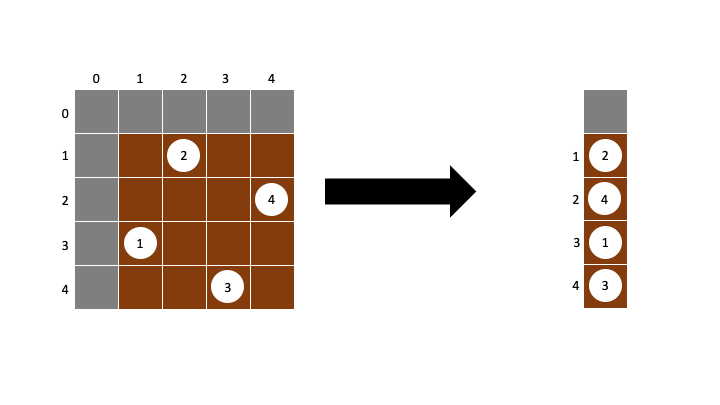
h=index
w=board[index]
def queens(n, board, h) :
ans = 0
if h == n :
return 1
for w in range(1, n+1) :
board[h + 1] = w
if promising(board, h+1) :
ans += queens(n, board, h+1)
return ans
def promising(board, h) :
for h_ in range(1, h) :
if (w_ := board[h_]) == (w := board[h]) or h - h_ == abs(w_ - w) :
return False
return True
solution = lambda n : queens(n, [0]*(n+1), 0)