줄 서는 방법

• 몫과 나머지

from math import factorial
solution = lambda n, k : recur([x for x in range(1, n+1)], k-1)
def recur(nums, k) :
    if (n := len(nums)) == 1 :
        return [nums.pop()]
    index, rest = divmod(k, factorial(n-1))
    return [nums.pop(index)] + recur(nums, rest)

몫과 나머지

n = 4 일때의 순열을 보자.

1로 시작하는 순열 \((4-1)!\)개

2로 시작하는 순열 \((4-1)!\)개

3로 시작하는 순열 \((4-1)!\)개

4로 시작하는 순열 \((4-1)!\)개

위 4개의 순열들을 0번부터 인덱스를 붙이고, k = 13이면 과연 몇으로 시작하는 순열에서 발견될까? 바로

k-1 // (4-1)! 인덱스 순열에 속하고, 그 순열에서 k-1 % (4-1)! 번째 순열이다.

• 첫번째 순열의 인덱스를 0으로 했기 때문에 k-1번째를 구해야함

무슨 말이냐 하면 내가 찾고자하는 13번째 수열은

index = 2
r = 0

3으로 시작하는 수열에서 0번째에 위치하게 된다.

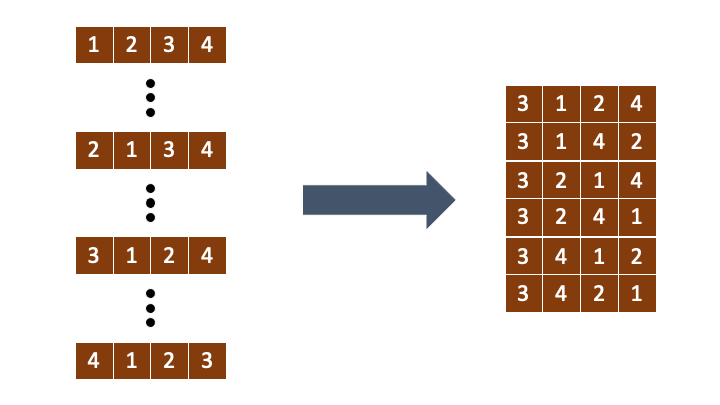
이 원리로 k-1을 \((n-1)!\) 로 나눈 몫과 나머지로 위치를 찾아가는 것이 핵심이다.