def solution(n, money):
money.sort()
dp = [0]*(n+1)
for m in money :
dp[m] += 1
for index in range(m+1, len(dp)) :
dp[index] += dp[index-m]
return dp[-1]
DP
전형적이고 대표적인 기본 DP문제다.
m-1개의 동전을 사용해n원을 만들때,m개의 동전으로는 몇개의n원을 만들 수 있을까
자세히는 모르겠지만, m-1개의 동전을 사용했을 때 만들 수 있는 동전조합과, m개의 동전을 사용했을 때 만들 수 있는 동전조합의 종류는 분명히 모종의 관계가 있을꺼라는 것을 직감적으로 알 수 있을것이다. 풀이를 들어가기 전에 이 부분만 확실하게 하고가자
오름차순으로 정렬된 동전종류 :
[a, b, c, ... n]
DP[1]: 동전a만사용 해서 만들 수 있는 거스름돈 종류
DP[2]: 동전 (a,b) 만 사용해서 만들 수 있는 거스름돈 종류
DP[3]: 동전 (a,b,c) 만 사용해서 만들 수 있는 거스름돈 종류
DP[n]: 동전 (a,b, …,n) 총n개의 동전을 사용해 만들 수 있는 거스름돈 종류
일반화를 하기위해 예시하나를 보자. 오름 차순으로 정렬된 동전종류 money = [3, 4, 5] 가 있고, 이 money로 15원을 만든다고 가정해 보자.
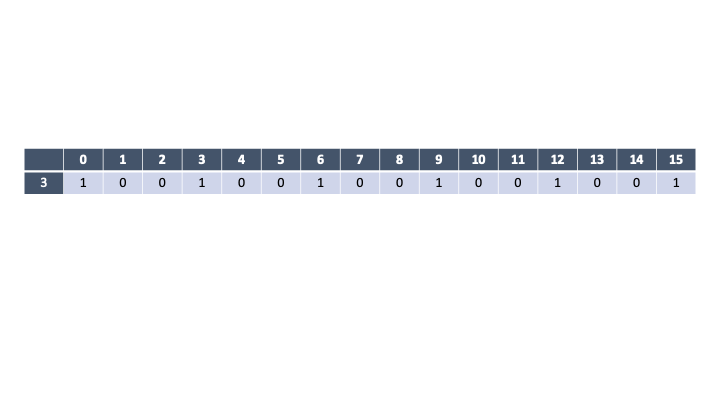
DP[1] 은 3의 배수일 경우에만 돈을 거슬러줄 수 있다.
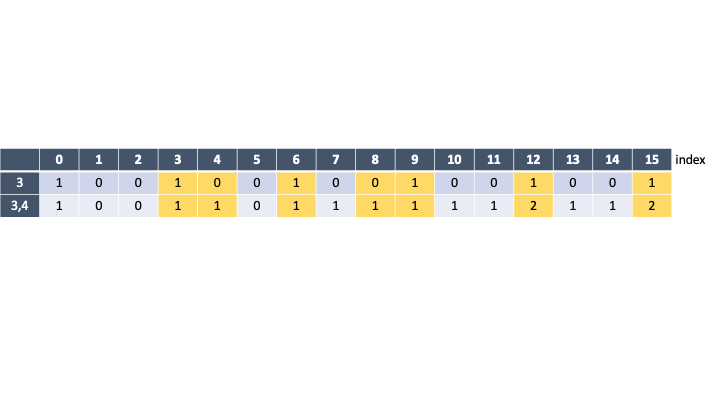
DP[2]부터 이게 어찌된 일인지 3, 4의 배수 말고도 만들 수 있는 동전 조합이 생겼다. 왜이렇게 되는지 살펴보자
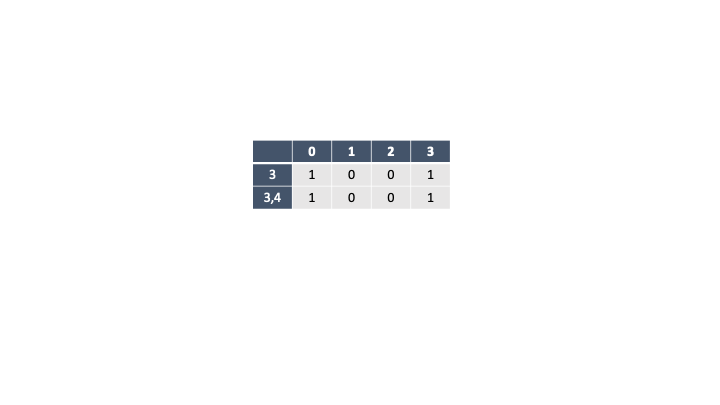
거스름돈이 4원 이전 까지는 기존의 3원의 조합과 동일하다.
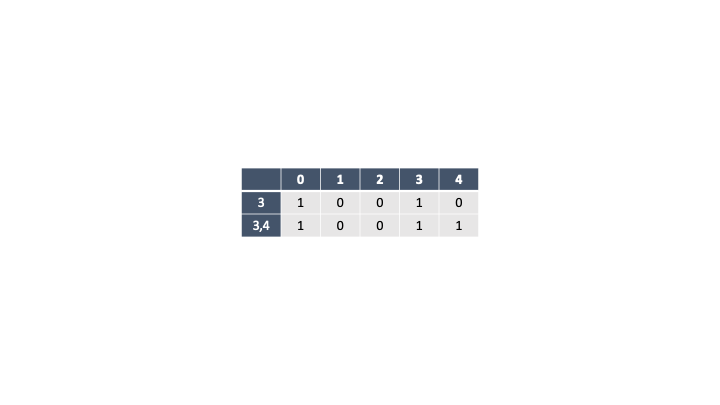
거스름돈 4원 부터 추가된 4원으로 만들 수 있으므로 조합하나가 추가된다.
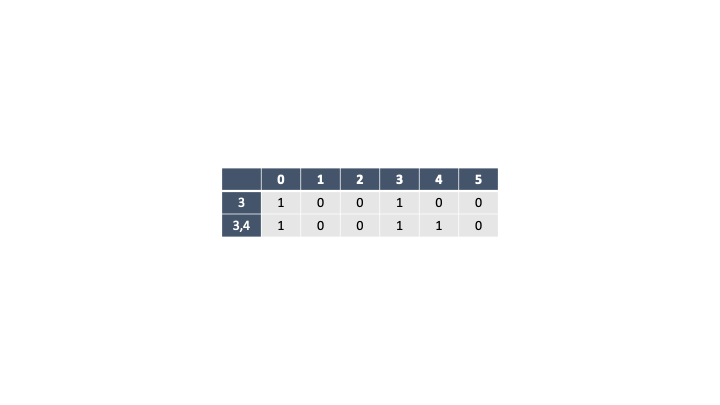
거스름돈 5원은 (3, 4) 조합으로 만들 수 없다. 왜그럴까? 거스름돈을 내주는 방식을 이렇게 정의해보자
일단 제일 큰 동전을 먼저 거슬러주고 뒷일은 차차 생각해야지ㅋ
5원의 경우 4원을 내주고 남은돈 1원을 거슬러줄 조합이 있을까? 우리는 다행이 1원을 거슬러줄 수 있는지에 대한 정보를 가지고 있다
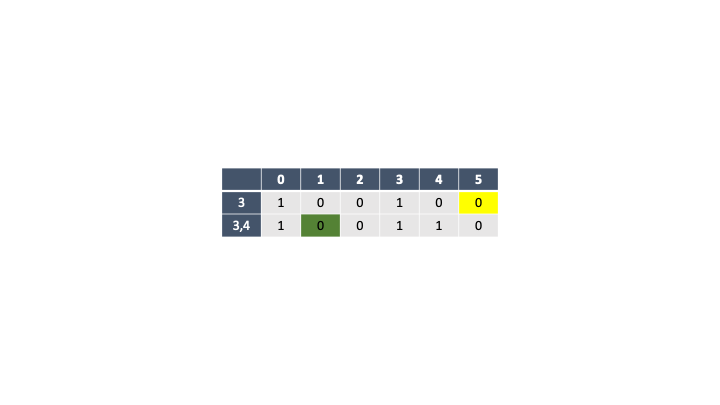
노란색이 현재 동전을 추가하기전 해당 돈을 거슬러 줄 수 있는 경우의 수이고 초록색이 가지고있는 가장 큰 동전을 하나 먼저 거슬러주고 남은 돈을 거슬러 줄 수 있는지에 대한 정보다. 0+0은 0이기 때문에 (3, 4) 조합으론 5원을 거슬러줄 수 없다.

6원의 경우 (현재 동전이 추가되기전 거슬러줄 수 있는 경우의수 1) + (4원 거슬러주고 남은 2 원 거슬러줄 수 있는 경우의수 0) = 1이 된다.

7원의 경우 (현재 동전이 추가되기전 거슬러줄 수 있는 경우의수 0) + (4원 거슬러주고 남은 3 원 거슬러줄 수 있는 경우의수 1) = 1이 된다.
패턴이 딱 나와버렸다. 그리고 현재 동전이 추가되기전 조합에 현재 동전이 추가된후의 경우의 수를 더하는 것이므로 기존의 DP배열에 현재 동전 거슬러주고 남은 돈을 거슬러 주는 경우의 수를 더해주면 된다.
DP[index] += DP[index - 현재동전]
def solution(n, money):
money.sort()
dp = [0]*(n+1)
for m in money :
dp[m] += 1 # 새로 m원이 추가되었으니 m원 거슬러줄 수 있으므로 +1
for index in range(m+1, len(dp)) : # 거슬러줄 돈 m+1 이상의 돈부터 공식을 사용
dp[index] += dp[index-m] # m : 현재 동전
return dp[-1]