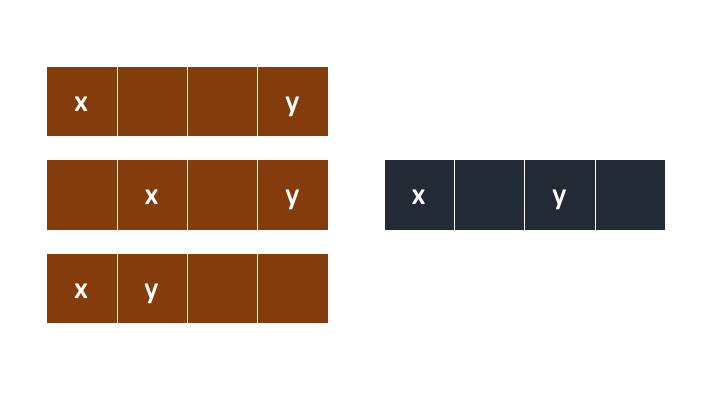from itertools import permutations
from collections import defaultdict
import copy
def solution(board, r, c):
global graph_, board_
answer = 1e9
graph = defaultdict(list)
for h in range(4) :
for w in range(4) :
if board[h][w] != 0 :
graph[board[h][w]].append([h, w])
for order in permutations(graph) :
que = [[r, c, 0]]
board_ = copy.deepcopy(board)
for v in order :
p1, p2 = graph[v]
for i in range(len(que)) :
h, w, cost = que.pop(0)
que.append(p1 + [cost + navigation([h, w], p2) + navigation(p2, p1)])
que.append(p2 + [cost + navigation([h, w], p1) + navigation(p1, p2)])
board_[p1[0]][p1[1]] = 0
board_[p2[0]][p2[1]] = 0
que.sort(key = lambda x : x[2])
answer = min(answer, que[0][2])
return answer + len(graph)*2
def navigation(p1, p2) :
h1, w1 = p1
h2, w2 = p2
return min(straight(board_[h1], w1, w2) + straight([x[w2] for x in board_], h1, h2), \
straight(board_[h2], w1, w2) + straight([x[w1] for x in board_], h1, h2))
def straight(list_, x, y) :
result = abs(x-y)
zeros = len([x for x in list_[min(x, y)+1:max(x, y)] if x == 0])
if result == 2 and list_[y] == 0 and 0<y<3 :
return result
return result - zeros
알고리즘
터트릴 카드 종류 순서 나열 후,
BFS탐색카드를 터트릴 때 최소로 움직일 조작
터트려야할 카드
터트릴 카드의 번호, 좌표를 저장할 사전을 생성 {index : [h, w]}
graph = defaultdict(list)
for h in range(4) :
for w in range(4) :
if board[h][w] != 0 :
graph[board[h][w]].append([h, w])
BFS
터트릴 카드의 모든 순열에대해 BFS 탐색을 하며 비용(조작횟수)이 가장 적게드는 답을 도출
for order in permutations(graph) :
que = [[r, c, 0]]
board_ = copy.deepcopy(board) # 순열 1개당 새로운 board가 필요하기 때문에 deepcopy
for v in order : # 순열에서 터트릴 카드 v
p1, p2 = graph[v] # v 카드 2개의 좌표값 p1, p2
for i in range(len(que)) : # BFS 탐색
h, w, cost = que.pop(0) # 현재 커서의 위치
que.append(p2의 좌표, 현재커서 -> p1 -> p2 터트리는 최소 비용)
que.append(p1의 좌표, 현재커서 -> p2 -> p1 터트리는 최소 비용)
board_[p1[0]][p1[1]] = 0 # 터트린 카드 v에대한 처리
board_[p2[0]][p2[1]] = 0 # 터트린 카드 v에대한 처리
que.sort(key = lambda x : x[2]) # 순열하나를 마쳤을 때의 전체비용
answer = min(answer, que[0][2]) # 순열 하나를 마쳤을 때 최소 비용갱신
커서 조작
현재 커서에서 카드의 위치로 움직일 수 있는 루트는 2가지 밖에없다.
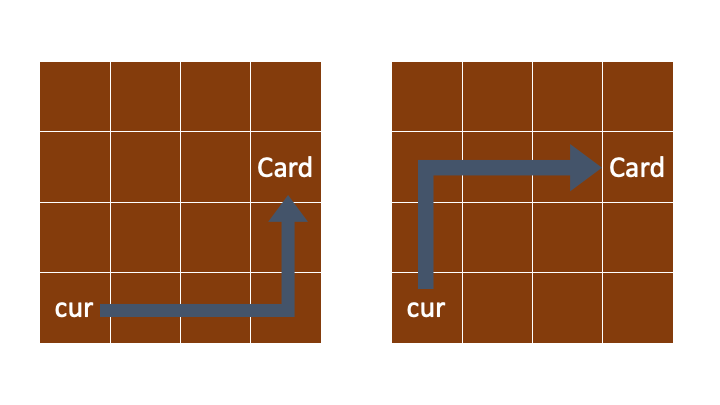
어떤 경로로 움직이는 것이 더 비용이 적게드는 지는 경로상에 무었이있는지, 그리고 카드 또는 커서의 위치가 벽에 붙어있는지 안쪽에있는지에 따라 다르다. 이렇게 생각하면 복잡하지만, 어떤경로를 선택하던지 간에 행으로 한번, 열로 한번 움직인다.

그렇다면 이렇게 경로를 나누어서 계산을 해주면 매우 쉽게 계산해 줄 수 있다.
straight
커서는 무조건 Ctrl+방향키 를 우선적으로 움직인다고 생각하자
왼쪽의 3가지 경우엔 x to y 의 조작 횟수는
y-x+빈칸의 갯수
- point
x와y위치에는 카드가 있을 수 도있고, 없을 수 도있다.
이다. 무조건적으로 Ctrl+방향키 를 우선적으로 쓰기 때문에 빈칸만 있다면 한방에가고, 그 사이에 카드가 있다면 x to y 거리에 빈칸의 갯수만큼 빼주면 된다. 하지만 오른쪽같은 경우엔 조금 다르게 생각해주어야한다.
y가 카드인 경우 : 왼쪽의 3가지 경우와 동일한 조작횟수를 가진다.
y가 빈칸인 경우 : 그냥x와y의 거리만큼 조작횟수가 필요함
이유는 조금만 깊게 생각해보면 이해할 수 있을꺼라 생각한다.
def navigation(p1, p2) :
h1, w1 = p1
h2, w2 = p2
return min(straight(board_[h1], w1, w2) + straight([x[w2] for x in board_], h1, h2), \
straight(board_[h2], w1, w2) + straight([x[w1] for x in board_], h1, h2))
def straight(list_, x, y) : # list_는 일자로 움직일 row, col을 때온것
result = abs(x-y) # x, y의 거리
zeros = len([x for x in list_[min(x, y)+1:max(x, y)] if x == 0]) # 0의 갯수
if result == 2 and list_[y] == 0 and 0<y<3 : # 오른쪽 케이스인데 y가 빈칸인 경우
return result
return result - zeros
이 두개의 함수가
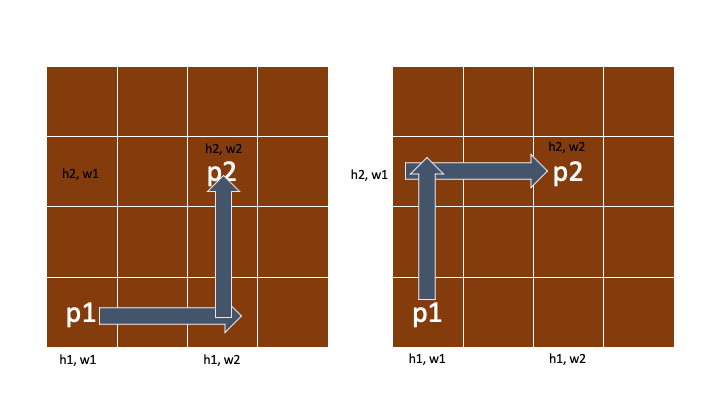
이것을 계산해주는 역할을 한다.
from itertools import permutations
from collections import defaultdict
import copy
def solution(board, r, c):
global graph_, board_
answer = 1e9
graph = defaultdict(list)
for h in range(4) :
for w in range(4) :
if board[h][w] != 0 :
graph[board[h][w]].append([h, w])
for order in permutations(graph) :
que = [[r, c, 0]]
board_ = copy.deepcopy(board)
for v in order :
p1, p2 = graph[v]
for i in range(len(que)) :
h, w, cost = que.pop(0)
# cursur -> p2 -> p1 가는 경로
que.append(p1 + [cost + navigation([h, w], p2) + navigation(p2, p1)])
# cursur -> p1 -> p2 가는 경로
que.append(p2 + [cost + navigation([h, w], p1) + navigation(p1, p2)])
board_[p1[0]][p1[1]] = 0
board_[p2[0]][p2[1]] = 0
que.sort(key = lambda x : x[2])
answer = min(answer, que[0][2])
return answer + len(graph)*2
def navigation(p1, p2) :
h1, w1 = p1
h2, w2 = p2
return min(straight(board_[h1], w1, w2) + straight([x[w2] for x in board_], h1, h2), \
straight(board_[h2], w1, w2) + straight([x[w1] for x in board_], h1, h2))
def straight(list_, x, y) :
result = abs(x-y)
zeros = len([x for x in list_[min(x, y)+1:max(x, y)] if x == 0])
if result == 2 and list_[y] == 0 and 0<y<3 :
return result
return result - zeros