풍선 터트리기
def solution(a):
answer = 2
l_min = a[0]
r_min = a[-1]
for i in range(1, len(a)-1) :
if l_min > a[i] :
answer += 1
l_min = a[i]
if r_min > a[len(a)-1-i] :
answer += 1
r_min = a[len(a)-1-i]
return answer -1 if l_min == r_min else answer
풀이
풍선을 터트릴 때 default로 큰 풍선부터 터트린다. 큰 풍선일수록 살아남기 힘들다는말.
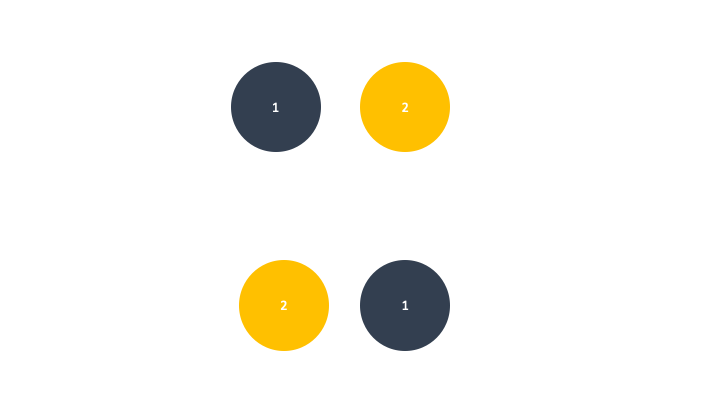
풍선이 2개 있을 땐 모든 풍선이 살아남을 수 있다.
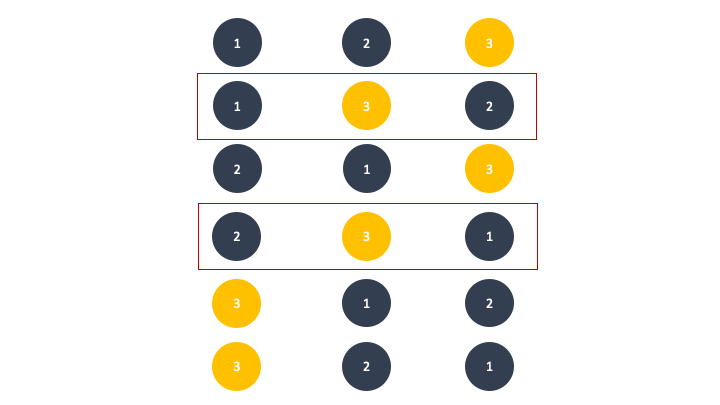
3개 부터 상황이 달라진다. 풍선 양옆이 자기보다 작은 풍선이면 그 풍선은 살아남지 못한다. 이 말의 대우는 살아남으려면 한쪽이 자기보다 큰 풍선이어야 한다 가 된다. 임의의 풍선이 살아남을 수 있는 케이스는
case 1 : 임의의 풍선이 양쪽 끝에 박혀있는 경우
- 임의의 풍선제외을하고 나머지 풍을 다 터트려 없앤 후 풍선이 2개만 남았을 때 작은 풍선 터트려 살아남기
case 2 : 임의의 풍선 한쪽이 자기보다 큰 풍선들만 있는 경우
- 찬스를 쓰지않고 한쪽풍선들을 싹다 정리할 수 있는경우
def solution(a):
answer = 2 # 양끝 풍선은 무조건 살아남으니 미리 추가
l_min = a[0] #왼쪽 끝풍선
r_min = a[-1] #오른쪽 끝풍선
for i in range(1, len(a)-1) : #
if l_min > a[i] : # 각 풍선마다 왼쪽이 자기보다 큰지
answer += 1
l_min = a[i]
if r_min > a[len(a)-1-i] : # 각 풍선마다 오른쪽이 자기보다 큰지
answer += 1
r_min = a[len(a)-1-i]
return answer -1 if l_min == r_min else answer # 같은 풍선검사 했을 경우 -1