가짜 해밀토니안

가짜 해밀토니안

다시 쓸예정. 참고ㄴㄴ

코드

import sys
sys.setrecursionlimit(400000)
from collections import defaultdict
def set_depth_subtree(node, prev) :
    sub_trees, depths = [], []
    for child in graph[node] :
        if child == prev : continue
        set_depth_subtree(child, node)
        sub_trees.append((sub_tree[child], child))
        depths.append((depth[child], child))
        depth[node] = max(depth[node], depth[child] + 1)
    sub_trees.sort(reverse=True)
    depths.sort(reverse=True)
    if len(sub_trees) >= 2 :
        if sub_trees[0][1] != depths[0][1] : sub_tree[node] = sub_trees[0][0] + depths[0][0] + 1
        else : sub_tree[node] = max(sub_trees[0][0] + depths[1][0] + 1, sub_trees[1][0]+depths[0][0] + 1)
    elif len(sub_trees) == 1 : sub_tree[node] = sub_trees[0][0] + 1


def DFS(node, prev, height) :
    global answer
    sub_trees, depths = [], []
    for child in graph[node] :
        if child == prev : continue
        sub_trees.append((sub_tree[child], child))
        depths.append((depth[child], child))
    sub_trees.sort(reverse=True)
    depths.sort(reverse=True)
    for child in graph[node] :
        if child == prev : continue
        next_height = height + 1
        if depths[0][1] != child :
            next_height = max(next_height, depths[0][0] + 2)
        elif len(depths) >= 2 and depths[0][1] == child :
            next_height = max(next_height, depths[1][0] + 2)
        DFS(child, node, next_height)
    if (len(sub_trees) >= 3) :
        answer = max(answer,
                     sub_trees[0][0]+sub_trees[1][0]+height,
                     sub_trees[0][0]+sub_trees[2][0]+depths[1][0]+1,
                     sub_trees[0][0]+sub_trees[1][0]+depths[2][0]+1)
    elif (len(sub_trees) == 2) :
        answer = max(answer, sub_trees[0][0]+sub_trees[1][0]+height)

def solution(t):
    global  answer, N, graph, sub_tree, depth
    N = len(t) + 1
    graph = defaultdict(list)
    sub_tree, depth = [1]*N, [1]*N
    answer = 0
    for v1, v2 in t:
        graph[v1].append(v2)
        graph[v2].append(v1)
    set_depth_subtree(0, -1)
    DFS(0, -1, 1)
    return answer

우선 가짜 해밀토니안 경로를 만족하는 그래프는 어떤 형태의 그래프인지 알아야합니다.

가짜 해밀토니안 경로 정의

경로가 그래프 상의 모든 점을 최소 1번, 최대 2번 방문해야 합니다.

같은 점을 두번넘게 방문 하지 않으려면

메인 경로가 하나 있고, 그 경로 상에 있는 모든 노드들에 대해서, 해당 노드에서 출발하는 일자형으로 뻗은 서브 경로가 최대 1개 있는 그래프

이런 모양을 트리형태로 바꿔보면

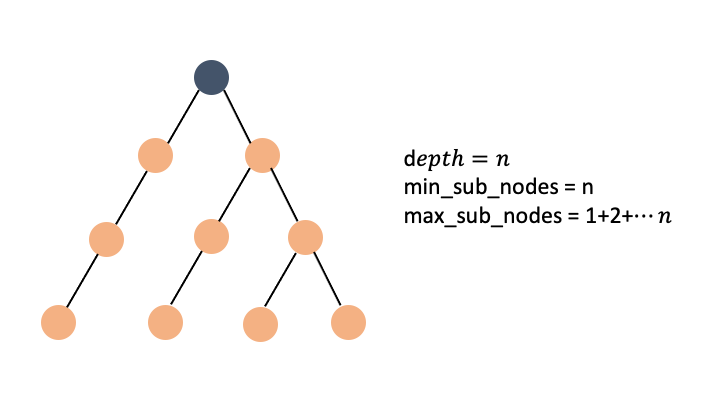
가짜 해밀토니안 경로를 만족하는 트리는 이런 이진트리 형태가 됩니다.

제한 사항

v1과 v2는 서로 다른 수입니다.

t는 항상 트리 형태로만 주어집니다.

입력값인 t 는 항상 트리 형태로 주어진다고 했습니다. 문제를 요약해보면

무작위로 주어진 트리형태의 그래프를 이런식으로 바꿔서 갯수를 return 하라는 문제가 됩니다. 하지만 큰 문제가 있습니다.

문제

Degree가 4이상인(자식이 3개 이상인) 노드는 어떻게 처리해야 하는가?

어떤 node 를 선택해야 가장 큰 해밀토니안 트리가 되는가?

생각만해도 머리가 깨질꺼같은 이 두가지 문제를 해결해야 합니다. 그냥 생각없이 계산한다면 n 개의 node 들로 이루어진 그래프일 경우 최악의 경우에는 \(n*2^{n}\) 번의 계산을 해야합니다.

가짜 해밀토니안 Tree

우선 Degree가 4개 이상인 노드를 어떻게 처리할지 생각해봅시다.

가짜 해밀토니안 tree의 모든 node 의 갯수는 Depth + num_sub_tree + 1 로 이루어져 있습니다. 그렇다면 주어진 그래프 t 에서 가장 큰 tree를 뽑아내려면 **각 node 의 자식들 중 Depth와 num_sub_tree가 가장 큰 자식들을 선택해야합니다. **

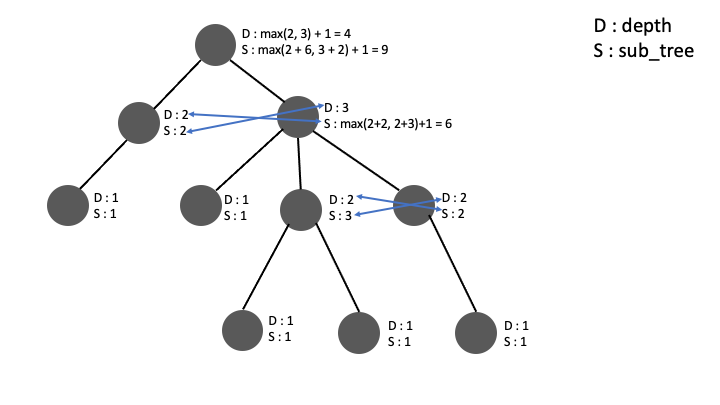
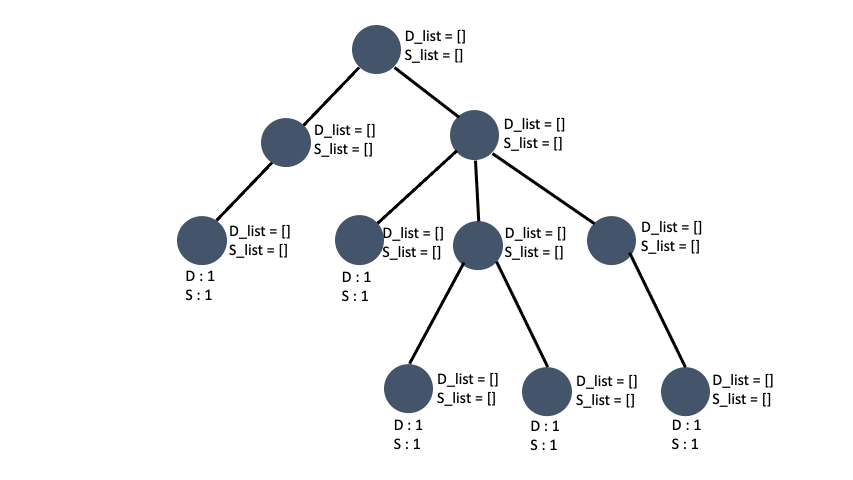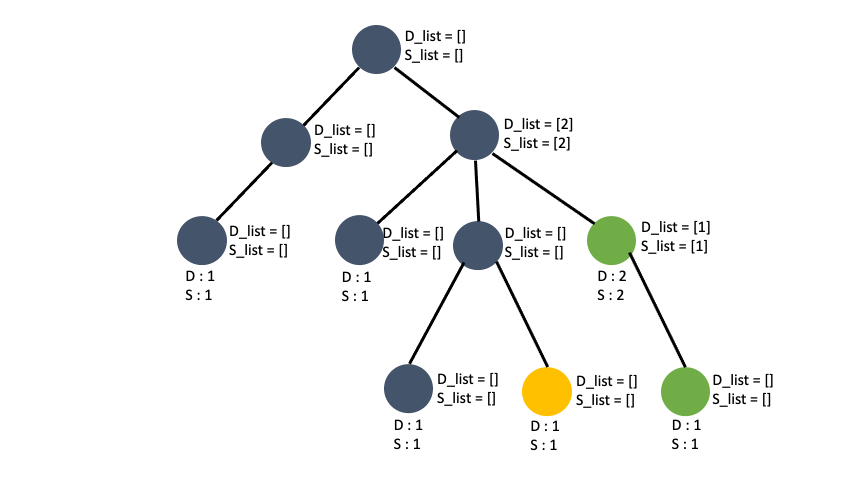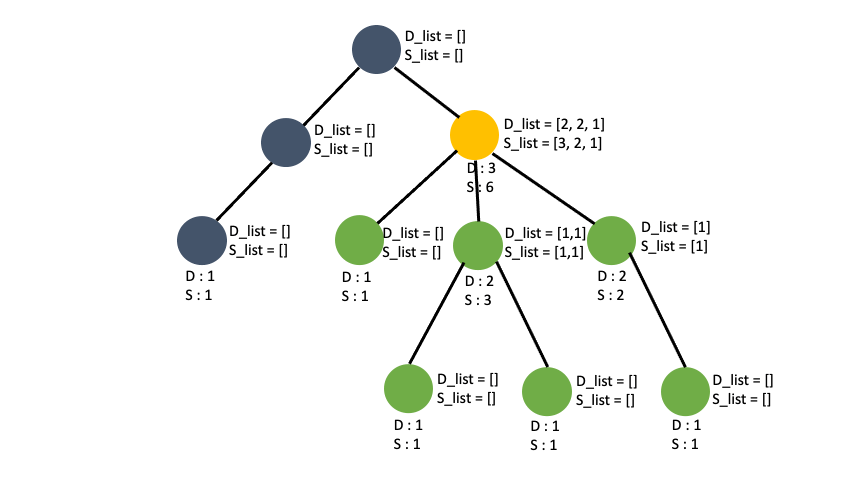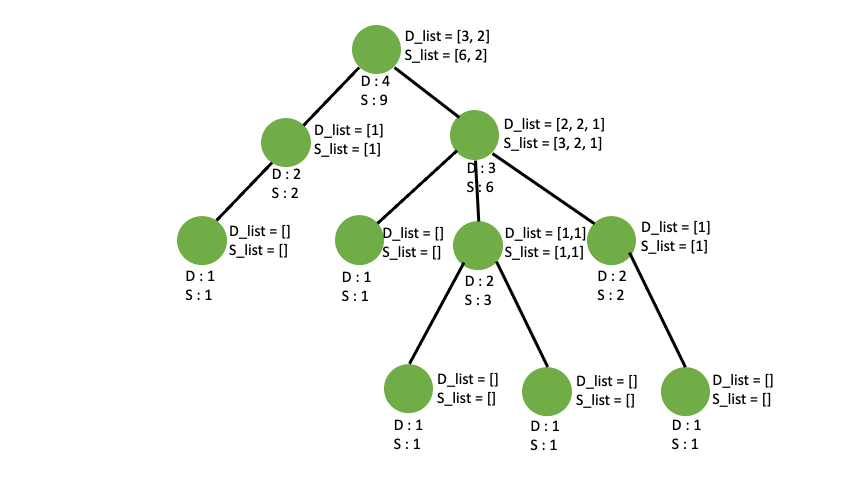
이런식으로 트리의 각 노드마다 Depth 와 sub_tree 갯수를 저장해가며 가장 큰 sub_tree 를 가지게 만들어줍니다.

def set_depth_subtree(node, prev) :
    sub_trees, depths = [], [] # 자식들의 깊이와 sub_tree 노드 갯수가 저장될 리스트
    for child in graph[node] :
        if child == prev : continue
        set_depth_subtree(child, node) # leaf로 들어가는 DFS
        sub_trees.append((sub_tree[child], child)) # node의 자식의 sub_tree 갯수 append
        depths.append((depth[child], child)) # node의 자식의 depth append
        depth[node] = max(depth[node], depth[child] + 1) # node의 depth 최신화
    sub_trees.sort(reverse=True) # sub_tree 내림차순 정렬
    depths.sort(reverse=True)  #depth 내림차순 정렬
    if len(sub_trees) >= 2 : # 자식이 2개 이상일 때
        if sub_trees[0][1] != depths[0][1] : # depth가 가장 큰 node와 sub_tree가 가장 큰 node가 다를 때
            sub_tree[node] = sub_trees[0][0] + depths[0][0] + 1
        else : #depth가 가장 큰 node와 sub_tree가 가장 큰 node가 같을 때
            sub_tree[node] = max(sub_trees[0][0] + depths[1][0] + 1, sub_trees[1][0]+depths[0][0] + 1)
    elif len(sub_trees) == 1 : sub_tree[node] = sub_trees[0][0] + 1

def solution(t):
    global  answer, N, graph, sub_tree, depth
    N = len(t) + 1
    graph = defaultdict(list)
    sub_tree, depth = [1]*N, [1]*N
    answer = 0
    for v1, v2 in t: # tree 그래프 생성
        graph[v1].append(v2)
        graph[v2].append(v1)
    set_depth_subtree(0, -1) # 임의의 노드에서 시작, 0 아니어도 상관없음
    return answer

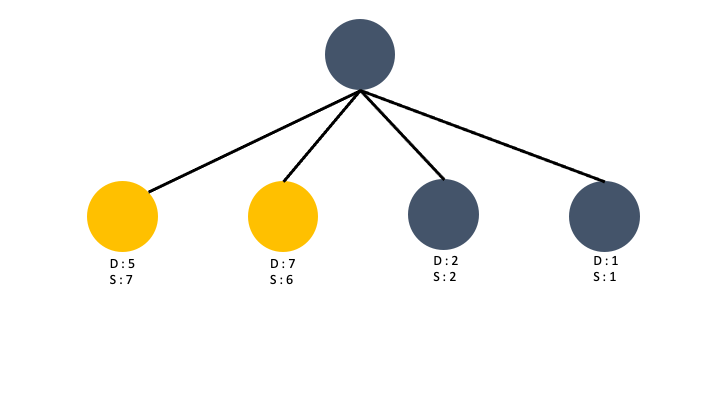
이렇게 Depth 가 가장 큰 노드와 Sub_tree 가 가장 큰 노드가 서로 다르면 그 둘을 선택하면 되지만

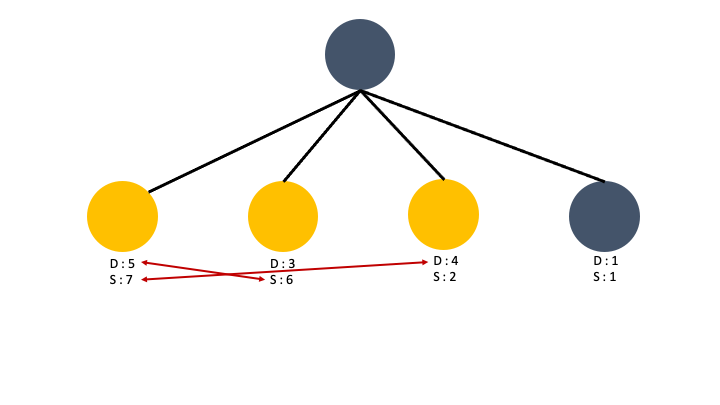
한 노드가 Depth 와 Sub_tree 둘다 가장 크다면 max(가장 큰 깊이 + 차선 서브트리, 가장 큰 서브트리 + 차선 깊이) 를 해주어야 합니다.

이렇게 임의의 노드를 기준으로 구성된 트리의 sub_tree 와 depth 정보들을 저장한 리스트를 DFS로 만들어 줍니다.

depth, sub_tree 만드는 과정

최대 subtree 값을 가지는 node 찾기

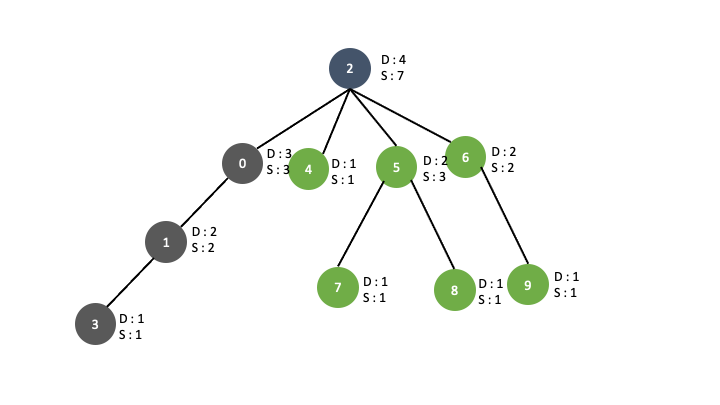
임의의 노드를 기준으로 트리를 완성시키고 각 노드를 취했을 때 얻을 수 있는 최대 depth, sub_tree를 구했습니다. 임의로 잡은 노드이기 때문에 그 트리의 root 의 sub_tree 갯수가 입력값 t 그래프의 갯수의 최대 sub_tree 인지 장담할 수 없습니다. 예를들면 이런 케이스가 있습니다.

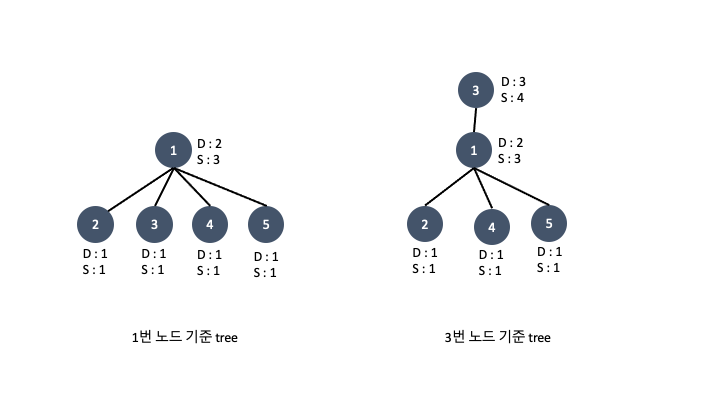
1번 노드를 기준으로 tree를 구성했을 때와 3번 노드를 기준으로 tree를 구성했을 때 root 의 sub_tree 의 갯수가 차이가 납니다. 그렇다고 **전체 노드에 대해서 DFS를 시행하면 중복된 depth 와 sub_tree 를 구하는 경우가 생기므로 시간초과나 런타임에러가 뜹니다. **

우선 가짜 해밀토니안 트리에서 노드하나를 떼서 봅시다.

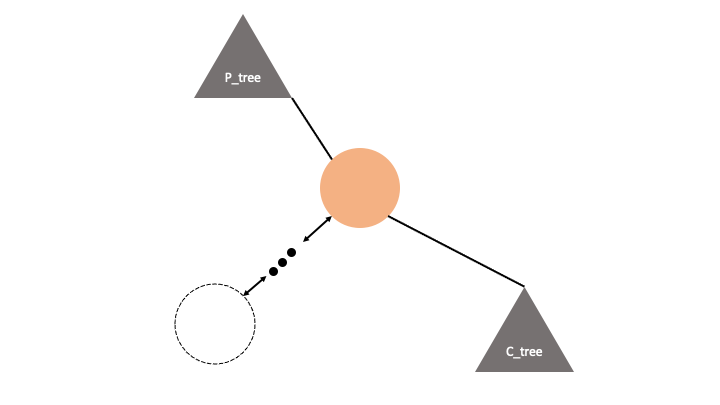
우리는 이 트리의 상태를 조금 다른 시각으로 볼 수 있습니다.

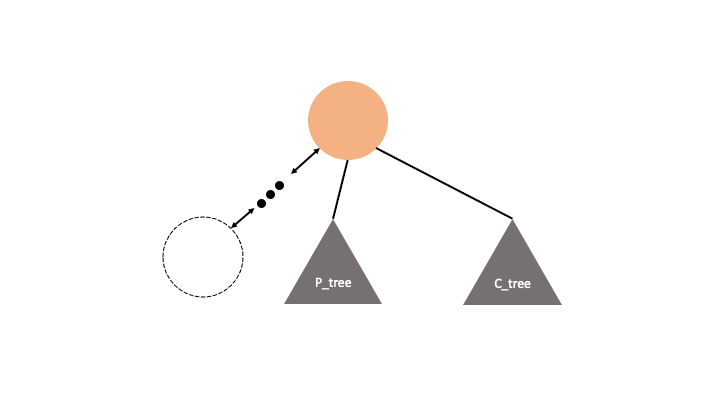
자기자신의 위쪽 sub tree를 아래쪽으로 내려서 마치 그 노드를 root 인것마냥 볼 수 있습니다.

그렇다면 내린 sub tree의 depth 와 sub_tree 의 갯수만 알면 전체 sub_tree 의 갯수를 알 수 있습니다.

height

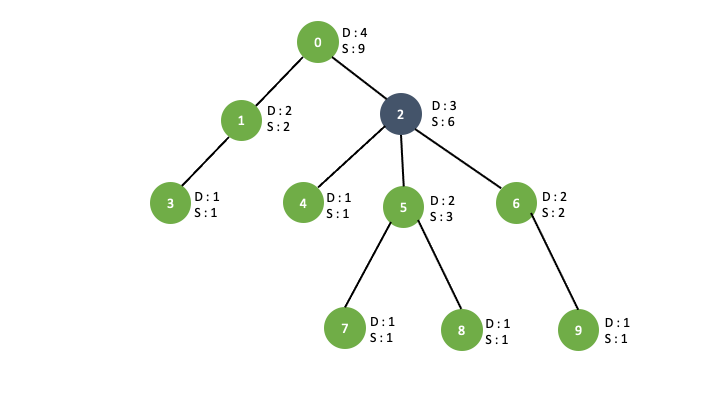
이미 0번을 루트로 만들어진 tree에서 2번 노드를 루트로 본다면, 0번 노드의 depth 는 max(0번 노드의 자식 중 2번 노드를 제외한 나머지 자식들의 높이) + 2가 됩니다. +2 가 되는 이유는

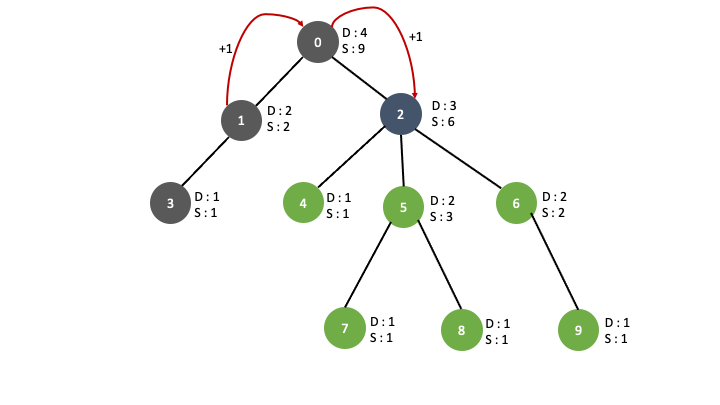
depth, sub_tree 만드는 과정

sub_tree 또한 마찬가지로 max(0번 노드의 자식 중 2번 노드를 제외한 나머지 자식들의 sub_tree) 이지만 구할 필요가 없습니다. depth 나 sub_tree 둘중 하나만 구하면 되는데 그 이유는 DFS 특성상 모든 자식 노드들에 돌아가며 depth, sub_tree 구하는 수행을 하기 때문에 자식노드의 부모 노드의 depth 와 sub_tree 를 계산하면 중복 계산이 일어납니다. 이거는 그림이나 말로 설명하기 어려우니 상상을 하며 코딩을 하시면서 이해하시길 바랍니다.

depth 계산이 더 쉬우므로 부모노드의 depth, 즉 height 를 구한뒤 기존 depth 와 height 중 큰것으로 depth 를 최신화 시켜주면 됩니다.

def DFS(node, prev, height) :
    global answer
    sub_trees, depths = [], []
    for child in graph[node] :
        if child == prev : continue
        sub_trees.append((sub_tree[child], child))
        depths.append((depth[child], child))
    sub_trees.sort(reverse=True)
    depths.sort(reverse=True)
    # node의 자식노드들에 대해서 높이 구하는 반복문
    for child in graph[node] :
        if child == prev : continue
        next_height = height + 1
        if depths[0][1] != child :
            next_height = max(next_height, depths[0][0] + 2)
        elif len(depths) >= 2 and depths[0][1] == child :
            next_height = max(next_height, depths[1][0] + 2)
        DFS(child, node, next_height)

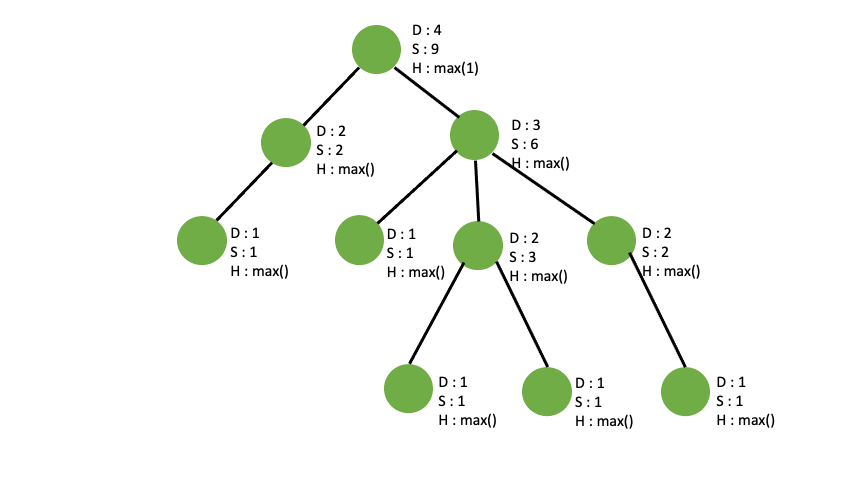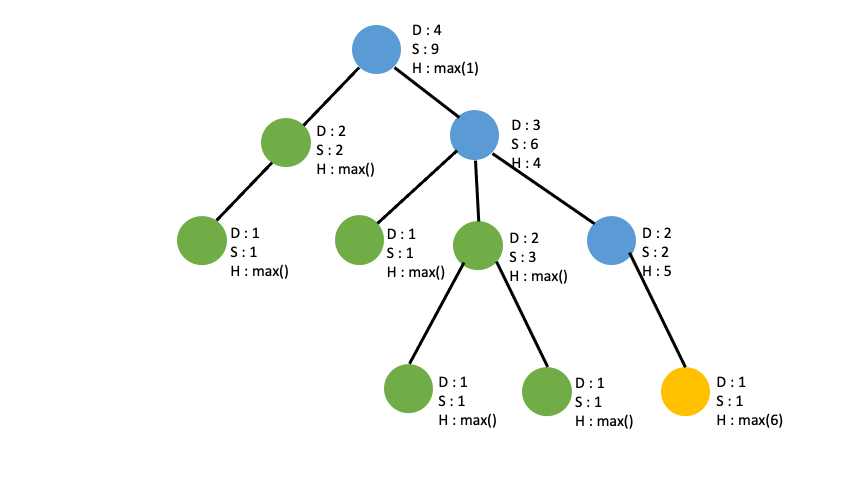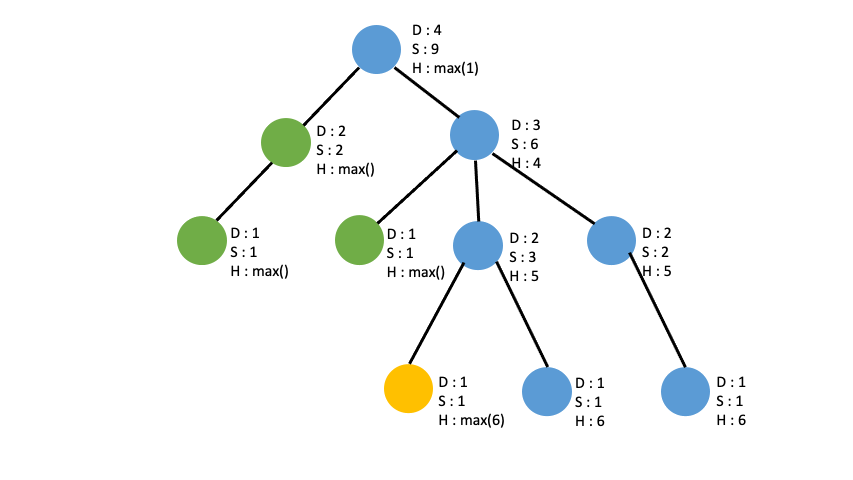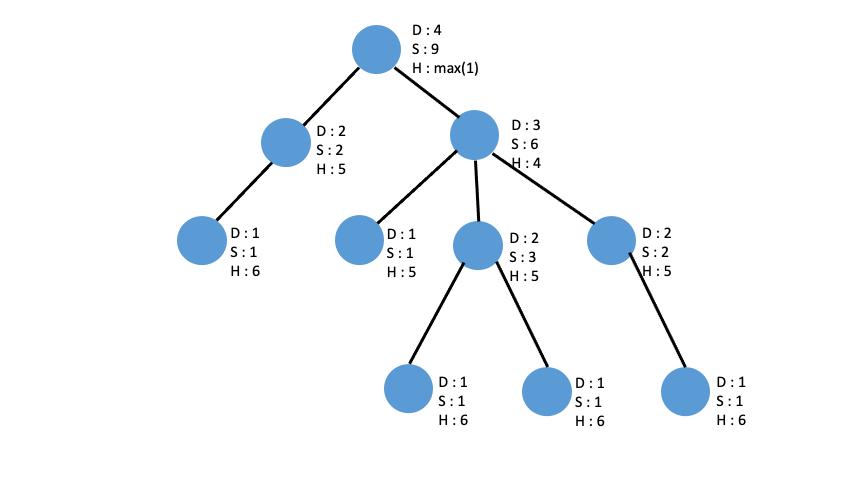
answer

각 node들에 대해서 height, depth, sub_tree 를 구했으니 가장 큰 값을 만드는 sub_tree 2개와 depth 를 찾으면 됩니다.

def DFS(node, prev, height) :
    global answer
    sub_trees, depths = [], []
    for child in graph[node] :
        if child == prev : continue
        sub_trees.append((sub_tree[child], child))
        depths.append((depth[child], child))
    sub_trees.sort(reverse=True)
    depths.sort(reverse=True)
    for child in graph[node] :
        if child == prev : continue
        next_height = height + 1
        if depths[0][1] != child :
            next_height = max(next_height, depths[0][0] + 2)
        elif len(depths) >= 2 and depths[0][1] == child :
            next_height = max(next_height, depths[1][0] + 2)
        DFS(child, node, next_height)

    # 정답을 찾는 부분
    # 각 노드들에 대해서 최대값을 return 하는 후보들중에서 max값 구하기
    if (len(sub_trees) >= 3) :
        answer = max(answer,
                     sub_trees[0][0]+sub_trees[1][0]+height,
                     sub_trees[0][0]+sub_trees[2][0]+depths[1][0]+1,
                     sub_trees[0][0]+sub_trees[1][0]+depths[2][0]+1)
    elif (len(sub_trees) == 2) :
        answer = max(answer, sub_trees[0][0]+sub_trees[1][0]+height)

가짜 해밀토니안

가짜 해밀토니안

코드

가짜 해밀토니안 경로 정의

제한 사항

문제

가짜 해밀토니안 Tree

최대 subtree 값을 가지는 node 찾기

height

answer

Comments