편집 거리(Edit Distance)
정확하게 기억은 나지 않지만 카카오 2020 겨울 인턴 코딩테스트에 편집거리에 관한 문제가 있었습니다.
편집거리는 두 단어의 유사도의 크기를 측정하는 단위입니다. 제 예상이지만 검색엔진에 잘못된 단어를 검색 했을 때, 단어를 추천해주는 알고리즘이 바로 편집거리 알고리즘이 아닐까 생각합니다.
두 단어 economy 와 yummy 를 한번 보겠습니다. 두 단어는 길이도 틀리고, 시작 알파벳도 틀립니다.
삽입 / 삭제 / 교체 비용

economy 를 수정해서 yummy 로 바꾸든, yummy 를 수정해서 economy 로 바꾸든 몇번의 수정이 필요할지는 몰라도 최단거리로 수정해야하는 횟수는 같습니다. economy 를 기준으로 단어를 수정한다면 이런 느낌으로 진행될 것입니다.

삽입 과 삭제 의 비용을 1 로 볼 때 교체 는 2가지 시각으로 봐야합니다.
- 같은 단어로 교체
- 다른 단어로 교체
같은 단어로 교체는 그 단어를 그대로 가지고 가는 것이기 때문에 비용을 0 으로 보아야 하고, 다른 단어로 교체할 경우 그 비용을 1 로 볼 수도 있지만 2 로 볼 수도 있습니다(교체\(=\) 삭제\(\rightarrow\)삽입 이기 때문).
교체 비용을 1 로 보든 2 로 보든 가중치는 마음대로 할 수 있지만, 같은 단어로 교체 비용을 0 으로 보는 시각은 중요합니다.
저는 교체비용을 2로 보겠습니다.
편집 거리
두 단어 A, B 의 편집과정 중에 나타나는 단어 X 를 보겠습니다.

min_edit_distance(A, B) == min_edit_distance(A, X) + min_edit_distance(X, B)
A 에서 B 로의 편집 거리는 (A, X) + (X, B) 입니다. 그런데 만약 A 의 길이가 B 의 길이보다 짧다면 A의 편집과정에선 무조건 삽입이 들어가야합니다. 반대로 A 의 길이가 B 의 길이보다 길다면 편집과정엔 무조건 삭제가 포함 되어야합니다. 그렇다면 우리는 단어 X 의 형태를 유추해 볼 수 있습니다.
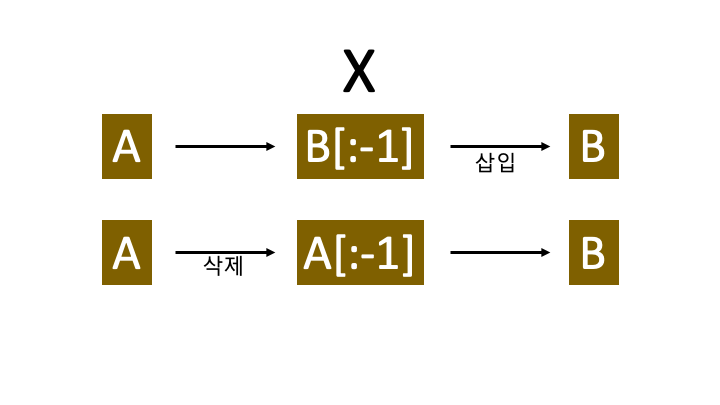
min_edit_distance(A, B) 에서 삽입, 삭제 가 필요한 경우의 비용을 다음과 같이 정리 할 수 있습니다.
# 삽입하는 경우 비용
min_edit_distance(A, B) = min_edit_distance(A, B[:-1]) + min_edit_distance(B[:-1], B)
# 삭제하는 경우 비용
min_edit_distance(A, B) = min_edit_distance(A, A[:-1]) + min_edit_distance(A[:-1], B)
이걸 다시 정리하면
# 삽입하는 경우 비용
min_edit_distance(A, B) = min_edit_distance(A, B[:-1]) + 1
# 삭제하는 경우 비용
min_edit_distance(A, B) = 1 + min_edit_distance(A[:-1], B)
이렇게 알고리즘을 정리할 수 있고, 교체의 경우는 2가지 시각이 있다고 말했습니다.
교체
- 같은 단어로 교체
- 다른 단어로 교체
교체 하고자하는 단어 index의 알파벳이 같으면 비용을 0, 다르다면 2 를 더해주면 됩니다.
하지만 편집거리 알고리즘은 왼쪽에서부터 오른쪽으로 비교를 해가며 단어를 삽입, 삭제, 교체를 하기 때문에 단어의 마지막 단어만 고려해 주면 됩니다.
# 교체하는 경우 비용
min_edit_distance(A, B) = min_edit_distance(A[:-1], B[:-1]) + 0 if A[-1]==B[-1] else 2
총 정리를 하면
# 삽입하는 경우 비용
min_edit_distance(A, B) = min_edit_distance(A, B[:-1]) + 1
# 삭제하는 경우 비용
min_edit_distance(A, B) = min_edit_distance(A[:-1], B) + 1
# 교체하는 경우 비용
min_edit_distance(A, B) = min_edit_distance(A[:-1], B[:-1]) + 0 if A[-1]==B[-1] else 2
# 최단거리 비용
min_edit_distance(A, B) = min(min_edit_distance(A, B[:-1]) + 1, #삽입
min_edit_distance(A[:-1], B) + 1, #삭제
min_edit_distance(A[:-1], B[:-1]) + 0 if A[-1]==B[-1] else 2) # 교체
우리는 단어가 어떻게 변해가는지는 관심없습니다, 두 단어의 편집거리가 얼만큼인지만 관심이 있기 때문에 비용만 고려했을 때 이런 알고리즘이 나옵니다.
편집거리 표
알고리즘을 구현하기 전에 편집거리 표를 만들겁니다.
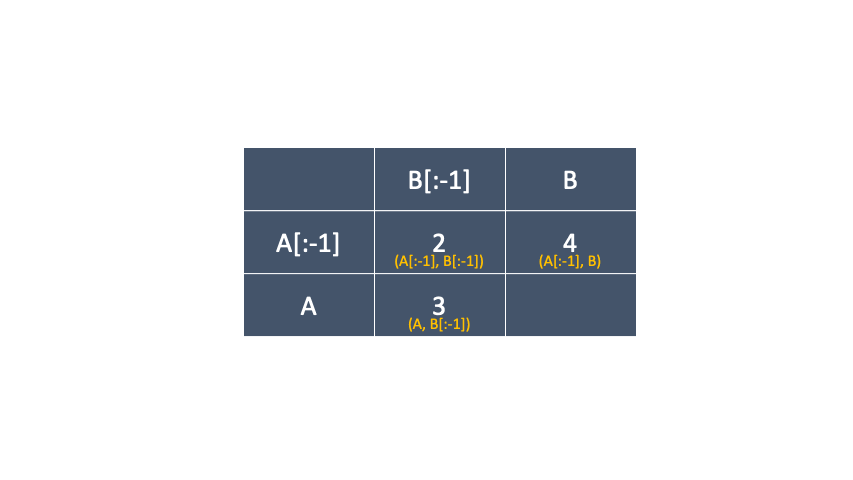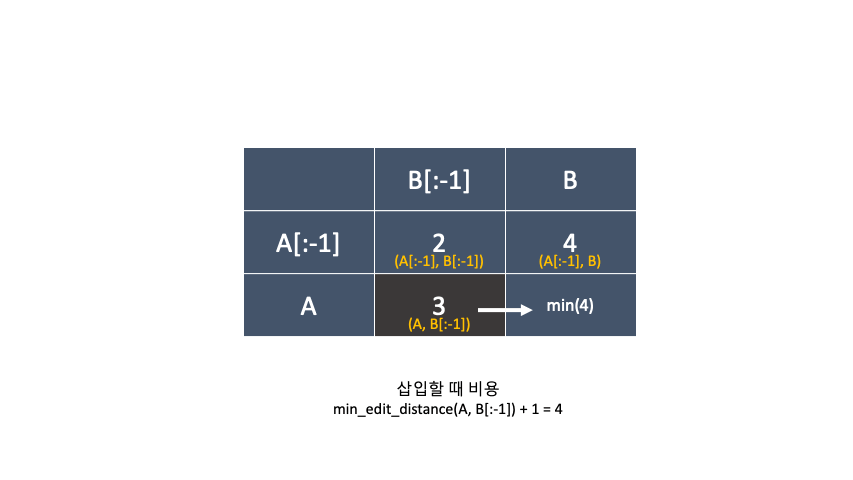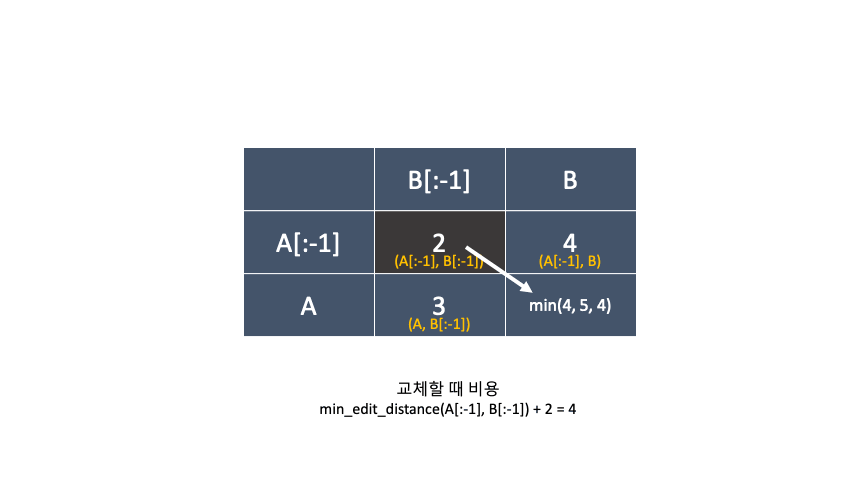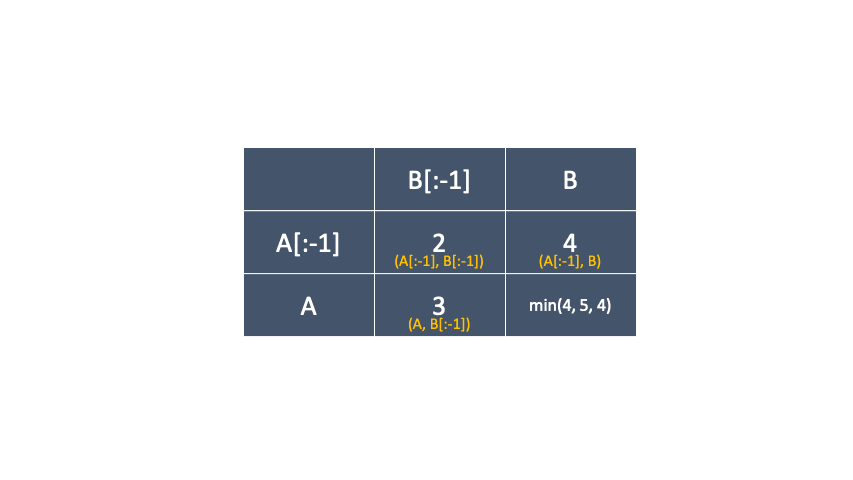
표는 이런식으로 구성될꺼고, 두 단어 ECONOMY 와 YUMMY 의 편집거리 표를 구해 보겠습니다.

삽입, 삭제, 교체 중 최소비용을 값을 계속 해서 채워나가는 방식인데, 교체 부분에서 알파벳이 같으면 +0 다르면 +2를 해주는 부분만 구별하면 됩니다.
편집거리 구현
코드는 다른분이 구현한 것을 참고했습니다.
import numpy as np
def minimum_edit_distance(source, target):
n = len(source)
m = len(target)
D = np.zeros((n+1, m+1))
# table build
for i in range(1, n+1):
D[i,0] = D[i-1,0] + deletion_cost(source[i-1])
for j in range(1, m+1):
D[0,j] = D[0, j-1] + insertion_cost(target[j-1])
# calculate edit distance
for i in range(1, n+1):
for j in range(1, m+1):
insert = D[i, j-1]
delete = D[i-1, j]
substitute = D[i-1, j-1]
D[i, j] = min(insert + 1,
delete + 1,
substitute + 0 if source[i-1]==target[j-1] else 2
)
return D[-1, -1]