블록 이동하기 풀이
코드
import numpy as np
from collections import deque
def sort_(state) : return sorted(state, key=lambda x : (x[0], x[1]))
def add(x, y) : return (x[0]+y[0], x[1]+y[1])
def check(head, tail) : return Board[head[0], head[1]] == 0 and Board[tail[0], tail[1]] == 0
def check_(state, move, cord) : return cord != state and cord not in move
def moving(head, tail) :
state = sort_([head, tail])
moving = [[1, 0], [-1, 0], [0, 1], [0, -1]]
move = [sort_([add(head,x), add(tail, x)]) for x in moving if check(add(head, x), add(tail, x))]
rotate = [sort_([head, add(head, x)]) for x in moving if check(head, add(head, x)) and check(tail, add(tail, x)) and check_(state, move, sort_([head, add(head, x)]))] +\
[sort_([tail, add(tail, x)]) for x in moving if check(head, add(head, x)) and check(tail, add(tail, x)) and check_(state, move, sort_([head, add(head, x)]))]
return move+rotate
def solution(board):
global Board, N
N = len(board)
Board = np.pad(board, ((1,1),(1,1)), 'constant', constant_values=1)
que = deque([[(1, 1), (1, 2), 0]])
visted = [[(1, 1), (1, 2)]]
while que:
head, tail, cost = que.popleft()
if head == (N, N) or tail == (N, N):
return cost
for child in moving(head, tail):
if child not in visted:
que.append([*child, cost+1])
visted.append(child)
이 문제에 관하여
혹시나 카카오 인턴 문제중 경주로 건설 을 풀어본 분들 느끼셨을지 모르지만 매우 유사한 문제입니다. 그 문제에서 회전이라는 기능과 칸 두개를 차지하고있는 차이점이 있습니다. 저는 항상 문제를 풀고 다른 사람들의 코드를 보며 다른 사람들의 코드를 공부하는데 이 문제는 제가 제일 깔끔하게 잘 푼것같습니다. 그 이유는 바로 로봇의 회전에대한 이해도 인것 같습니다. 일단 회전을 하기전에 일단 상,하,좌,우 움직임부터 보겠습니다.
상, 하, 좌, 우
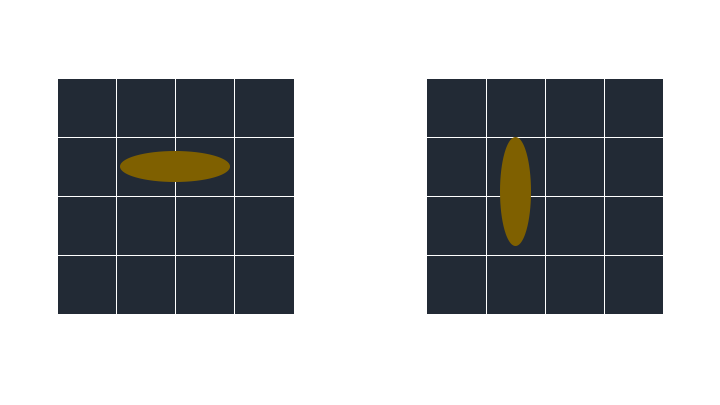
이 상태에서 상, 하, 좌, 우로 갈 수있는 움직임은 각각 4가지 입니다.
로봇의 좌상단을 항상 head로 놓고 본다면 로봇은 세로이든 가로이든 이런식으로 코딩됩니다.
(head+[0, 1], tail + [0, 1]) # 오른쪽으로 이동
(head+[0, -1], tail + [0, -1]) # 왼쪽으로 이동
(head+[-1, 0], tail + [-1, 0]) # 위로 이동
(head+[1, 0], tail + [1, 0]) # 아래로 이동
물론 numpy.array를 쓰지않으면 저런식으로 head+[0, 1]해주는 것은 불가능 하지만 일단 개념적으로 그렇다는 겁니다.
이런 식으로 움직임에 대한 다음 좌표들을 간단하게 만들 수있습니다.
# 실제 코드가 아닌 수도 코드라고 생각해 주시면 됩니다.
moving = [[1, 0], [-1, 0], [0, 1], [0, -1]]
move = [(head + x, tail + x) for x in moving]
이렇게 하면 위, 아래, 좌, 우 에대한 로봇의 다음 좌표가 완성됩니다.
회전
이 문제는 겉보기엔 로봇이 가로일 때의 회전과 세로일 때의 회전을 따로 구별해서 코딩을 해야하는것 같지만 사실 그렇지 않습니다.

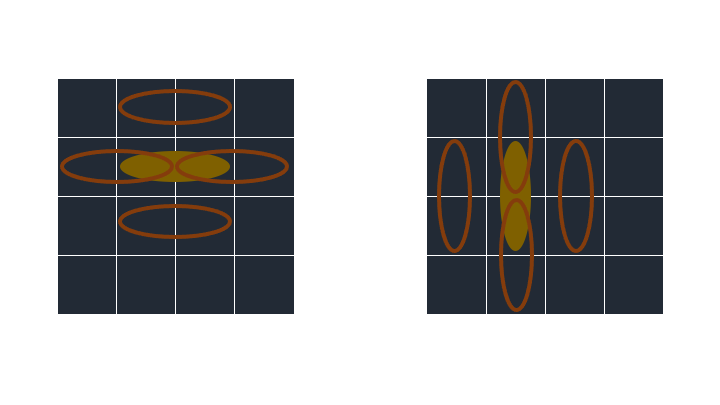
이 가로/세로 상태에서 로봇은 각각 4가지씩 회전을 가질 수 있습니다.
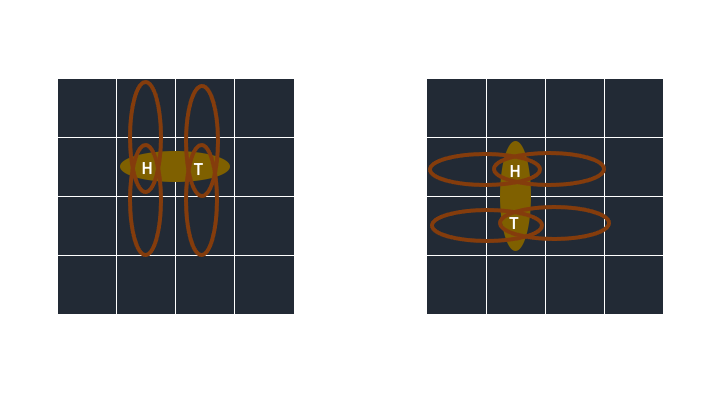
로봇이 가로일 때
(head, head + [-1, 0]) # head기준 반시계 회전
(head, head + [1, 0]) # head기준 시계 회전
(tail, tail + [-1, 0]) # tail기준 시계 회전
(tail, tail + [1, 0]) # tail기준 반시계 회전
로봇이 세로일 때
(head, head + [0, 1]) # head기준 반시계 회전
(head, head + [0, -1]) # head기준 시계 회전
(tail, tail + [0, 1]) # tail기준 시계 회전
(tail, tail + [0, -1]) # tail기준 반시계 회전
패턴이 보이시나요?
가로일 때
- (회전축, 회전축 +
([1, 0] or [-1, 0]))세로일 때
- (회전축, 회전축 +
([0, 1] or [0, -1]))
그럼 만약에 로봇이 가로일 때 세로 회전방식을 쓰고, 로봇이 세로일 때 가로 회전방식을 쓴다면 어떻게 변할까요.
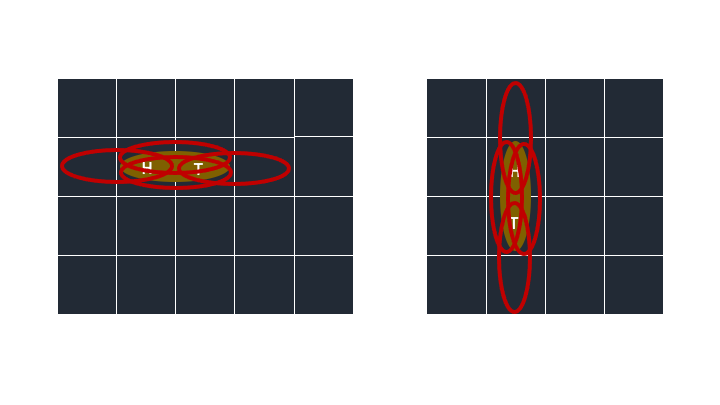
이렇게 가로일 때 세로회전을 쓰면 좌, 우, 기존 (head, tail) 2개가 나오고, 세로일 때 가로회전을 쓰면 상, 하, 기존 (head, tail) 2개 가 나옵니다.
# 실제 코드가 아닌 수도 코드라고 생각해 주시면 됩니다.
moving = [[1, 0], [-1, 0], [0, 1], [0, -1]]
move = [(head + x, tail + x) for x in moving] # 상하좌우
rotate = [(head, head + x) for x in moving] + [(tail, tail + x) for x in moving] # 회전
이런식으로 회전을 가로일 때, 세로일 때 조건을 나누지 않고 move를 만든 것 처럼 똑같이 코딩을 한다면 총 8개의 회전이 적용된 (head, tail)좌표가 나오고, 나온 8개의 좌표 중 2개의 좌표는 move 와 겹치고 다른 2개의 좌표는 기존의 (head, tail) 좌표와 겹칩니다.
그리고 rotate에서 중복된 4개의 좌표만 걸러주면 굳이 복잡하게 if로 가로/세로 나누어주지 않고도 회전된 좌표를 뽑을 수 있습니다.
sort
이 문제를 풀때 sort는 필수입니다. 왜냐하면 ((1, 2), (1, 3))과 ((1, 3), (1, 2))은 같은 상태이기 때문에 구별되면 안됩니다. 그래야지만 rotate에서 중복된 좌표들을 걸러낼 수 있기 때문입니다. 예를들면
state = [(2, 3), (2, 2)] # 기존 위치
move = [[(2, 3), (2, 4)], #우로 이동
[(2, 1), (2, 2)], #좌로 이동
[(1, 2), (1, 3)], #위로 이동
[(3, 2), (3, 3)]] #아래 이동
rotate = [[(2, 3), (3, 3)], #head 반시계
[(2, 3), (1, 3)], #head 시계
[(2, 3), (3, 3)], #tail 시계
[(4, 3), (3, 3)], #tail 반시계
[(2, 3), (2, 2)], #기존 위치
[(2, 2), (2, 3)], #기존 위치
[(2, 4), (2, 3)], #우로 이동
[(2, 2), (2, 1)]] #좌로 이동
이런상태에서 각 좌표가 정렬되어 있지 않으면 중복을 걸러낼 수 가 없습니다. 따라서 모든 좌표는 sort를 한 후에 move 나 rotate에 넣어야 합니다.
check
move
이동한 좌표
head나tail중 하나라도 벽(1)위에 있으면 안되므로head, tail둘다board[i, j] == 0인 곳으로만 움직이도록 해야합니다.rotate
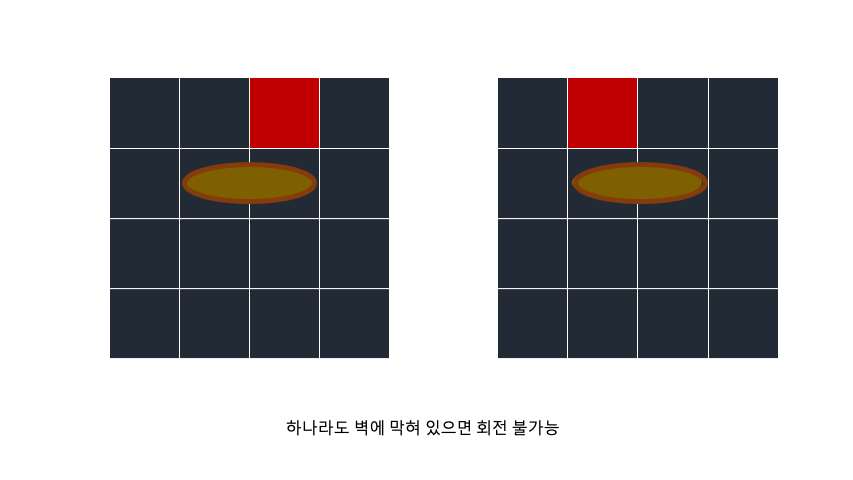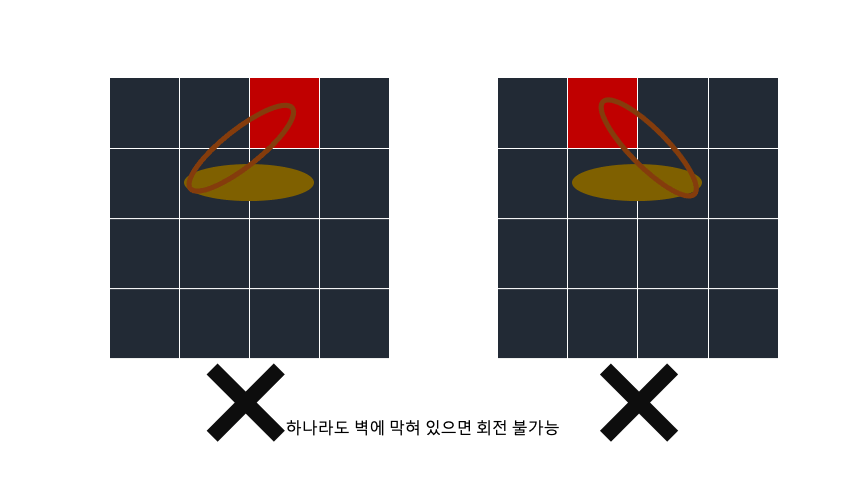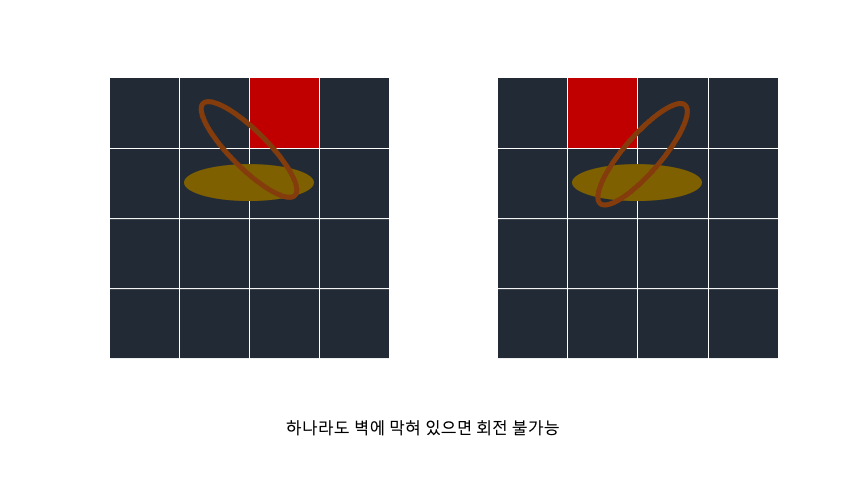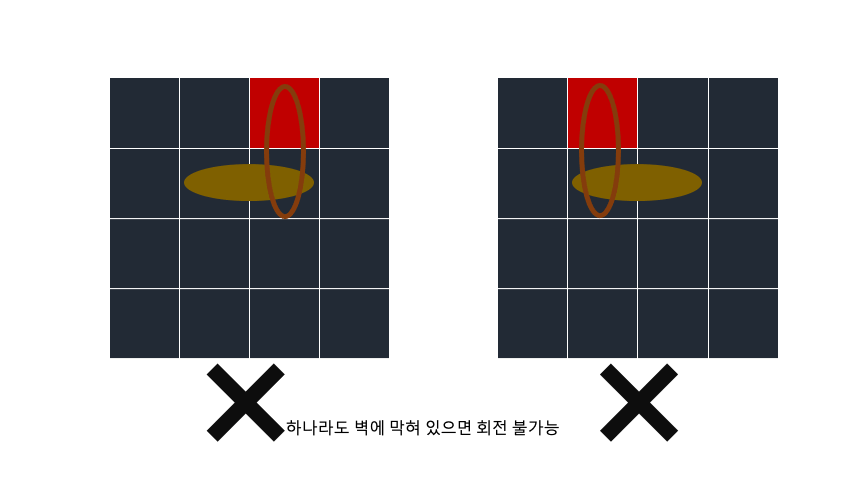
회전 축을 기준으로 어느 하나라도 벽에 막혀있으면 회전 불가능
이것을 바탕으로 코딩을 해보면 일단
def sort_(state) : return sorted(state, key=lambda x : (x[0], x[1]))
def add(x, y) : return (x[0]+y[0], x[1]+y[1])
def check(head, tail) : return Board[head[0], head[1]] == 0 and Board[tail[0], tail[1]] == 0 # 벽위 설치 체크
def check_(state, move, cord) : return cord != state and cord not in move # 중복 체크
기본 4가지 함수 sort, add, check, check_를 간단하게 만들 수 있습니다.
def moving(head, tail) :
state = [head, tail]
moving = [[1, 0], [-1, 0], [0, 1], [0, -1]]
move = [[add(head,x), add(tail, x)] for x in moving]
rotate = [[head, add(head, x)] for x in moving] + \
[[tail, add(tail, x)] for x in moving]
return move+rotating
그리고 이렇게 아무런 제약을 주지않은 move와 rotate를 코딩합니다. 그리고 먼저 중복 제거를 하기위해 모든 (head, tail)을 정렬 해줍니다.
def moving(head, tail) :
state = sort_([head, tail]) # sort 적용
moving = [[1, 0], [-1, 0], [0, 1], [0, -1]]
move = [sort_([add(head,x), add(tail, x)]) for x in moving] # sort 적용
rotate = [sort_([head, add(head, x)]) for x in moving] +\ # sort 적용
[sort_([tail, add(tail, x)]) for x in moving] # sort 적용
return move+rotate
그리고 먼저 move와 rotate에 대해서 벽위에 위치해 있지 않도록 제약을 줍니다.
def moving(head, tail) :
state = sort_([head, tail])
moving = [[1, 0], [-1, 0], [0, 1], [0, -1]]
move = [sort_([add(head,x), add(tail, x)]) for x in moving if check(add(head, x), add(tail, x))] # 제약 추가
rotate = [sort_([head, add(head, x)]) for x in moving if check(head, add(head, x)) and check(tail, add(tail, x))] +\ # 제약 추가
[sort_([tail, add(tail, x)]) for x in moving if check(head, add(head, x)) and check(tail, add(tail, x))] # 제약 추가
return move+rotate
rotate 경우에는 회전하고자 하는 방향 두칸모두다 벽이 없어야하기에 check를 두번 적용한 것입니다.
그리고 마지막으로 rotate에서 check_ 를 이용해 중복 제약을 걸어줍니다.
def moving(head, tail) :
state = sort_([head, tail])
moving = [[1, 0], [-1, 0], [0, 1], [0, -1]]
move = [sort_([add(head,x), add(tail, x)]) for x in moving if check(add(head, x), add(tail, x))]
rotate = [sort_([head, add(head, x)]) for x in moving if check(head, add(head, x)) and check(tail, add(tail, x)) and check_(state, move, sort_([head, add(head, x)]))] +\
[sort_([tail, add(tail, x)]) for x in moving if check(head, add(head, x)) and check(tail, add(tail, x)) and check_(state, move, sort_([head, add(head, x)]))]
return move+rotate
solution
나머지 BFS로 경로찾기는 워낙 흔하고 쉽기 때문에 다른분의 코드를 참고했습니다. board에 굳이 패딩을 안해줘도 되지만 고치기 귀찮아서 저도 그대로 썼습니다. 이해하는데 크게 어려움이 없으실 것으로 생각됩니다.
def solution(board):
global Board, N
N = len(board)
Board = np.pad(board, ((1,1),(1,1)), 'constant', constant_values=1)
que = deque([[(1, 1), (1, 2), 0]])
visted = [[(1, 1), (1, 2)]]
while que:
head, tail, cost = que.popleft()
if head == (N, N) or tail == (N, N):
return cost
for child in moving(head, tail):
if child not in visted:
que.append([*child, cost+1])
visted.append(child)
딱 한가지 que.append([*child, cost+1]) 이 부분에서 *child 이거는 자세히는 모르지만 직접해보니 느낌은 알 수 있습니다..
from collections import deque
a = [(1, 2), (2,3)]
b = deque()
b.append([*a, 3])
b.append([a, 3])
for i in b :
print(i)
[(1, 2), (2, 3), 3] [[(1, 2), (2, 3)], 3]
*를 붙이면 묶여있는것을 풀고 합쳐서 append해주는 기능 하나 봅니다.