동굴 탐험 풀이
동굴 탐험 문제 바로가기 이 문제는 어떻게 풀어야할지 감이 안잡혀서 풀이 해설을 봤지만… 해설대로 구현을 해도 효율성에서 계속 막혀서 성공한 사람의 코드중 김현우님의 코드가 가장 잘 짠거같아서 그분의 코드를 이해하고 공부했습니다.
코드 (by.김현우)
import sys
sys.setrecursionlimit(10**6)# 재귀 깊이 설정
def haveCycle(node):
if visit[node]:
if visit[node] == -1:
return True
return False
visit[node] = -1
for _next in inv_graph[node]:
if haveCycle(_next):
return True
visit[node] = 1
return False
def make_inv_graph(node, parent):
for child in graph[node]:
if child != parent:
inv_graph[child].append(node)
make_inv_graph(child, node)
def solution(n, path, order):
global graph, inv_graph, visit
graph, inv_graph, visit = [[] for _ in range(n)], [[] for _ in range(n)], [0]*n
for parent, node in path:
graph[parent].append(node)
graph[node].append(parent)
make_inv_graph(0, -1)
for parent, node in order:
inv_graph[node].append(parent)
for node in range(n):
if haveCycle(node):
return False
return True
문제에 관하여
이번 문제는 크게 2가지 풀이가 있는것 같습니다.
- 사전 조건에 하에
DFSorBFS로 모든 방이 탐색 가능한가? - 역방향 그래프를 만들고 탈출이 가능한가?
저는 개인적으로 역방향 그래프를 이용한 풀이가 더 센스있고, 출제자의 의도와 부합하기에 이 풀이법을 선택했습니다.
마치 우리가 미로탐험을 할때 도착지에서 출발지로 거꾸로 탐험하며 길을 찾듯이 역방향으로 탐색을 하는 것입니다.
이번 문제코딩의 가장 중요한 부분은 2가지
- 역방향 그래프 만들기
- 역방향 그래프 탐색
입니다.
역방향 그래프
def solution(n, path, order):
global graph, inv_graph, visit #Global 변수 설정
graph, inv_graph, visit = [[] for _ in range(n)], [[] for _ in range(n)], [0]*n
return True
우선 path 무방향 그래프를 만들어줍니다.
def solution(n, path, order):
global graph, inv_graph, visit
graph, inv_graph, visit = [[] for _ in range(n)], [[] for _ in range(n)], [0]*n
for a, b, in path : # 무방향 그래프 생성
graph[a].append(b)
graph[b].append(a)
return True
자, 이런 그래프가 만들어졌습니다.

루트노드를 제외한 모든 노드는 {부모, 자식}을 가리키고 있습니다. 역방향 그래프는 노드에서 부모 엣지만 골라내어 새로운 그래프를 만들면 됩니다.

def makeDirectedGraph(node, parent):
for child in adj[node]:
if child != parent:
directedGraph[child].append(node)
makeDirectedGraph(child, node)

def solution(n, path, order):
global graph, inv_graph, visit
graph, inv_graph, visit = [[] for _ in range(n)], [[] for _ in range(n)], [0]*n
for parent, node in path:
graph[parent].append(node)
graph[node].append(parent)
make_inv_graph(0, -1) # 역방향 그래프
return True
재귀를통해 현재 node의 엣지들 중 parent node를 가리키는 엣지를 제외하고 child node가 현재 node를 가리키게 하면 됩니다.
제한 사항 추가
order의 내용(선방문이 필요한 노드들)을 순서가 반대로 inv_graph에 넣어줍니다(역방향 그래프이기 때문에).
def solution(n, path, order):
global graph, inv_graph, visit
graph, inv_graph, visit = [[] for _ in range(n)], [[] for _ in range(n)], [0]*n
for parent, node in path:
graph[parent].append(node)
graph[node].append(parent)
make_inv_graph(0, -1)
for parent, node in order: # 제한 사항 추가
inv_graph[node].append(parent)
return True
inv_graph 탐색
역방향 그래프를 만든 이유는 도착지에서 출발지로 갈 수 있는지를 확인하기 위해서 입니다. 동굴탐험이 가능하려면 어떤 노드에서 출발해도 도착지(0번노드)로 도착이 가능해야합니다. 만약 탈출이 불가능하다면 0번노드로 도착하지못하고 빙빙도는 cycle이 생길 것입니다.
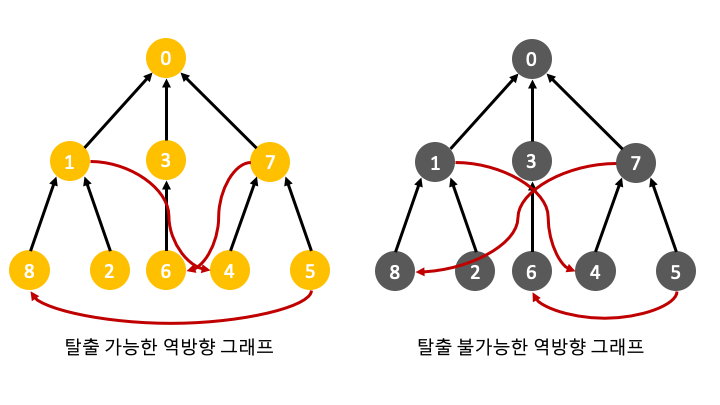
제한사항이 추가된 역방향 그래프를 탐색해 cycle을 찾아내야합니다.
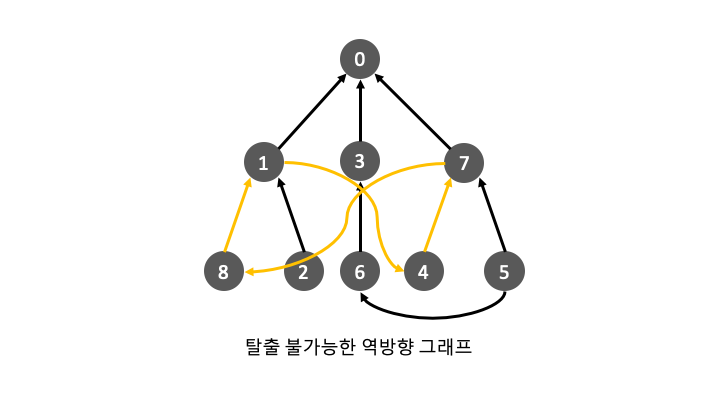
일반 DFS알고리즘에서 cycle의 존재를 확인하는 방법을 추가해야하기 때문에 DFS를 변형 해야합니다.
제한사항이 추가된 노드는 엣지가 2개이기 때문에 갈래길이 생깁니다. 만약 cycle이 존재한다면 한쪽 갈래길은 무사히 출발지(0번노드)로 가겠지만, 다른 갈랫길은 탐색도중에 다시 그 노드로 돌아올 것 입니다.
visit의 상태는 탐색전(0), 탐색완료(1), 탐색중(-1)의 상태를 가집니다.- 탐색중일 때 같은노드를 2번 방문하게 된다면
cycle이므로True를 리턴하고 종료합니다.- 탐색중일 때 탐색완료된 노드를 방문하게 된다면
False를 리턴하고 종료합니다.
def haveCycle(node): # 파이썬은 0 == False 로 인식함.
if visit[node]:
if visit[node] == -1:
return True
return False
visit[node] = -1
for _next in inv_graph[node]:
if haveCycle(_next):
return True
visit[node] = 1
return False
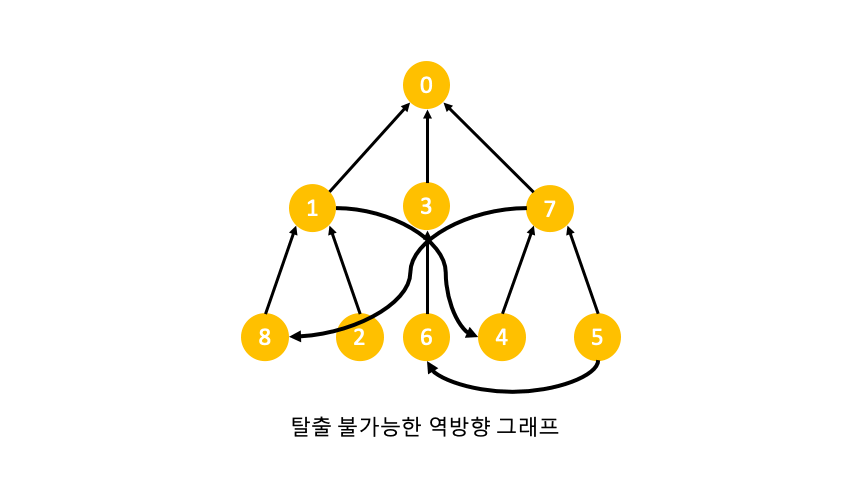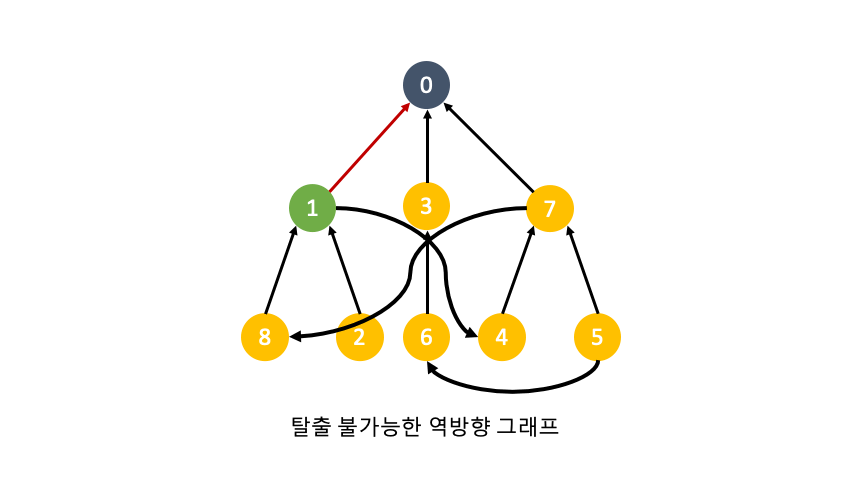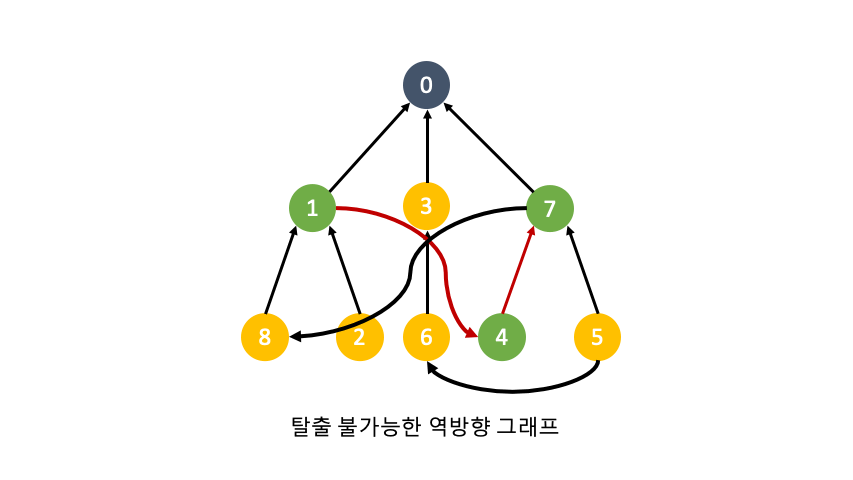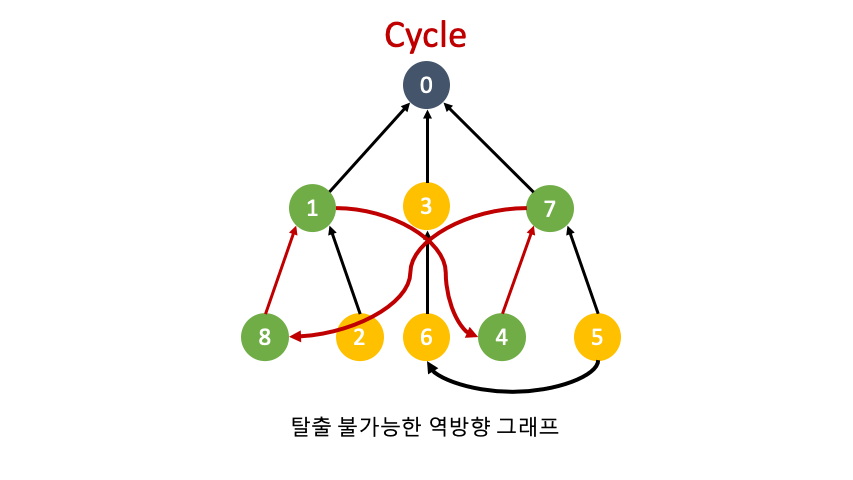

0번 노드부터 n번 노드까지 haveCycle 함수를 이용해 탈출 여부를 판별합니다.
import sys
sys.setrecursionlimit(10**6) # 재귀 깊이 설정
def haveCycle(node):
if visit[node]:
if visit[node] == -1:
return True
return False
visit[node] = -1
for _next in inv_graph[node]:
if haveCycle(_next):
return True
visit[node] = 1
return False
def make_inv_graph(node, parent):
for child in graph[node]:
if child != parent:
inv_graph[child].append(node)
make_inv_graph(child, node)
def solution(n, path, order):
global graph, inv_graph, visit
graph, inv_graph, visit = [[] for _ in range(n)], [[] for _ in range(n)], [0]*n
for parent, node in path:
graph[parent].append(node)
graph[node].append(parent)
make_inv_graph(0, -1)
for parent, node in order:
inv_graph[node].append(parent)
for node in range(n):
if haveCycle(node):
return False
return True